Electromagnetic radiation, a cornerstone of physics, manifests as waves characterized by specific attributes. These attributes, vital for understanding phenomena analyzed at institutions like MIT, influence everything from fiber optic communication to spectroscopy. The distance between repeating units of a wave, specifically measured from a wavelength crest trough, defines its wavelength crest trough and fundamentally impacts its interaction with matter. An understanding of wavelength crest trough enables scientists to determine an understanding and analyze wave behavior, using tools like the spectrometer, and helps identify the properties of matter.
Waves are not confined to the ocean’s surface; they are a fundamental aspect of the universe, permeating everything from the smallest subatomic particles to the vast expanse of space. Consider the light that allows us to see, the sound that allows us to hear, and even the radio waves that connect us globally. All of these phenomena are propagated through waves.
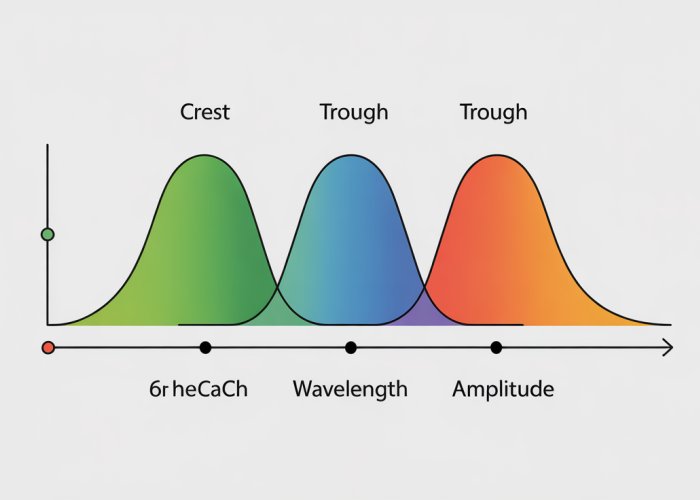
Understanding the characteristics of waves is essential to unraveling the mysteries of the physical world. This article aims to provide a comprehensive explanation of three key components of wave behavior: wavelength, crests, and troughs.
The Ubiquitous Nature of Waves
From the gentle ripples in a pond to the powerful shockwaves of an earthquake, waves manifest in diverse forms and scales.
Electromagnetic radiation, including visible light, travels in the form of waves, carrying energy across vast distances.
Sound, on the other hand, propagates through the vibration of particles in a medium, creating pressure waves that our ears interpret as sound.
Even at the quantum level, particles exhibit wave-like properties, blurring the lines between matter and energy.
Unveiling the Core Components: Wavelength, Crests, and Troughs
This discussion will center on clearly defining and illustrating the key elements that constitute a wave.
We will dissect the anatomy of a wave, focusing on:
-
Wavelength: The distance between two identical points on successive waves.
-
Crests: The highest points of a wave.
-
Troughs: The lowest points of a wave.
By understanding these fundamental components, we can begin to grasp the behavior and properties of waves.
A Glimpse Beyond: Amplitude, Frequency, and Wave Types
While this article primarily focuses on wavelength, crests, and troughs, it’s important to acknowledge the broader context of wave phenomena.
Other crucial concepts include:
-
Amplitude: The maximum displacement of a wave from its equilibrium position, dictating wave intensity.
-
Frequency: The number of wave cycles per unit of time, influencing wave energy.
Furthermore, waves can be classified into various types, such as transverse and longitudinal waves, each exhibiting unique characteristics and behaviors. The electromagnetic spectrum, encompassing radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays, further exemplifies the diversity of wave phenomena, each characterized by a specific wavelength and frequency. These topics, while not the primary focus, will be briefly touched upon to provide a more complete picture of the world of waves.
Waves are ubiquitous, but to truly understand their impact and behavior, it’s essential to dissect their fundamental components. Let’s embark on a journey to explore the core elements that define a wave: wavelength, crests, and troughs.
The Anatomy of a Wave: Crests, Troughs, and Wavelength Defined
This section will delve into the specific definitions of wavelength, crests, and troughs, visualizing these concepts to improve your comprehension. Further, we will understand their collective importance in determining wave behavior.
Defining the Wavelength
Formal Definition
Wavelength is formally defined as the distance between two successive points in phase on a wave.
These points could be two crests, two troughs, or any two identical points on consecutive waves.
Think of it as the length of one complete wave cycle.
Visual Representation
Imagine a series of ocean waves.
The wavelength is the distance from the peak of one wave to the peak of the next.
A diagram illustrating this concept typically shows a sinusoidal wave, with the wavelength clearly marked as the distance between two adjacent crests or troughs.
Visualizing the wave in this way makes understanding the wavelength more intuitive.
Crests and Troughs
Crests
The crest of a wave is the highest point of the wave above the line of zero displacement.
It represents the point of maximum positive displacement.
Troughs
Conversely, the trough of a wave is the lowest point of the wave below the line of zero displacement.
This is the point of maximum negative displacement.
Importance
Crests and troughs are not just high and low points; they play a crucial role in determining wave energy and behavior.
The amplitude, which is directly related to the height of the crest or depth of the trough, is a measure of the wave’s energy.
Waves with higher crests and deeper troughs carry more energy.
Understanding crests and troughs helps us interpret the power and potential impact of a wave.
Relationship with Amplitude
Amplitude Defined
Amplitude is the maximum displacement of a wave from its equilibrium position.
It’s a measure of how far the wave deviates from its resting state.
Connection
The amplitude is directly related to the crest and trough.
Specifically, amplitude is measured from the zero line (the equilibrium position) to the crest or to the trough.
A wave with a large amplitude will have high crests and deep troughs.
Understanding the relationship between amplitude, crests, and troughs provides a comprehensive understanding of wave strength and energy.
Crests and troughs, along with wavelength, paint a vivid picture of a single wave. However, a wave’s behavior isn’t solely determined by its spatial characteristics. The rate at which these waves oscillate, or their frequency, plays an equally crucial role. Let’s examine this concept and its fascinating relationship with wavelength.
Frequency and Wavelength: An Inverse Relationship
Frequency introduces the element of time into our understanding of waves. It quantifies how rapidly a wave oscillates, impacting how we perceive and interact with wave phenomena. This section delves into the definition of frequency, its units of measurement, and most importantly, its inverse relationship with wavelength, all tied together by the elegant wave equation.
Defining Frequency
At its core, frequency describes the repetition rate of a wave.
Formal Definition
Formally, frequency is defined as the number of complete wave cycles that pass a given point in one second. This definition highlights the dynamic nature of waves, emphasizing their movement and oscillation over time.
Units of Measurement: Hertz (Hz)
The standard unit for measuring frequency is the Hertz (Hz), named after the German physicist Heinrich Hertz.
One Hertz is equivalent to one cycle per second.
Therefore, a wave with a frequency of 10 Hz completes ten full cycles every second. Higher frequency values indicate more rapid oscillations, while lower frequencies correspond to slower oscillations. Common prefixes are often used, such as kilohertz (kHz) for thousands of cycles per second and megahertz (MHz) for millions of cycles per second.
The Inverse Relationship Between Frequency and Wavelength
Frequency and wavelength are inextricably linked, exhibiting an inverse relationship. This means that as frequency increases, wavelength decreases, and vice versa, assuming the wave’s velocity remains constant.
Imagine shaking a rope to create a wave. If you shake it faster (increasing the frequency), the distance between the crests (the wavelength) becomes shorter. Conversely, shaking the rope slower results in a longer wavelength.
The Wave Equation: v = fλ
This inverse relationship is elegantly captured in the wave equation:
v = fλ
Where:
- v represents the wave’s velocity (speed).
- f represents the frequency.
- λ (lambda) represents the wavelength.
This equation is a cornerstone of wave physics, demonstrating that the velocity of a wave is the product of its frequency and wavelength. If the velocity v is constant, then f and λ must be inversely proportional.
For example, consider light waves traveling through a vacuum, where the speed of light (c) is constant. If the frequency of the light increases (shifting towards the blue end of the spectrum), the wavelength must decrease.
Similarly, if the wavelength increases (shifting towards the red end of the spectrum), the frequency must decrease.
Applying Physics Concepts to Explain Wave Phenomena
The inverse relationship between frequency and wavelength helps explain a wide range of wave phenomena.
For instance, in the context of sound waves, higher frequency sounds (like a high-pitched whistle) have shorter wavelengths, while lower frequency sounds (like a deep bass) have longer wavelengths.
This difference in wavelength affects how these sounds interact with objects and how our ears perceive them.
Similarly, in the electromagnetic spectrum, radio waves have long wavelengths and low frequencies, while gamma rays have extremely short wavelengths and high frequencies.
Understanding the relationship between frequency and wavelength is crucial for analyzing and manipulating wave behavior in various applications, from communication technologies to medical imaging.
Crests and troughs, along with wavelength, paint a vivid picture of a single wave. However, a wave’s behavior isn’t solely determined by its spatial characteristics. The rate at which these waves oscillate, or their frequency, plays an equally crucial role. Let’s examine this concept and its fascinating relationship with wavelength.
Wave Types and Wavelength Characteristics Across the Spectrum
The concept of wavelength gains even greater significance when we consider the vast array of wave types that exist in nature. Waves aren’t limited to the idealized sine waves we often use for illustration. They manifest in various forms, each with unique properties and behaviors dictated by its wavelength and frequency.
This section explores how wavelength varies across different types of waves, with a focus on the electromagnetic spectrum and sound waves.
The Electromagnetic Spectrum: A Wavelength Wonderland
The electromagnetic (EM) spectrum is a continuum of all possible electromagnetic radiation frequencies. From incredibly long radio waves to extremely short gamma rays, the EM spectrum encompasses a staggering range of wavelengths, each corresponding to a different type of EM radiation.
Diving into Different Waves
Different types of waves within the electromagnetic spectrum (radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays) possess distinctly different wavelengths and frequencies.
Radio waves, with their long wavelengths (ranging from millimeters to hundreds of meters), are used for broadcasting, communication, and radar.
Microwaves have shorter wavelengths (roughly 1 millimeter to 1 meter) and are employed in microwave ovens, satellite communications, and Wi-Fi technology.
Infrared radiation, with wavelengths shorter than microwaves but longer than visible light, is associated with heat and is used in thermal imaging and remote controls.
Visible Light: A Rainbow of Wavelengths
Visible light, the portion of the EM spectrum that our eyes can detect, comprises a narrow band of wavelengths ranging from approximately 400 nanometers (violet) to 700 nanometers (red).
Each wavelength within this range corresponds to a different color.
Shorter wavelengths are perceived as violet and blue, while longer wavelengths are seen as orange and red. The combination of all these wavelengths creates white light.
Ultraviolet (UV) radiation has shorter wavelengths than visible light and can cause sunburns and skin cancer.
X-rays have even shorter wavelengths and are used in medical imaging to visualize bones and internal organs.
Finally, gamma rays, with the shortest wavelengths and highest frequencies, are produced by nuclear reactions and are used in cancer treatment.
Sound Waves: Wavelength and Pitch
Sound waves, unlike electromagnetic waves, are mechanical waves that require a medium (such as air, water, or solids) to propagate. They are longitudinal waves, meaning that the particles of the medium vibrate parallel to the direction of wave propagation.
The wavelength of a sound wave is related to its pitch. Short wavelengths correspond to high-pitched sounds, while long wavelengths correspond to low-pitched sounds.
For example, a piccolo produces high-pitched sounds with short wavelengths, whereas a tuba produces low-pitched sounds with long wavelengths. The human ear can typically detect sound waves with frequencies ranging from 20 Hz to 20,000 Hz, corresponding to wavelengths ranging from approximately 17 millimeters to 17 meters in air.
Wave Propagation: Sine and Cosine’s Dance
Wave propagation describes how a wave transfers energy through a medium. It is the process by which disturbances travel from one point to another. Understanding wave propagation is fundamental to comprehending wave behavior.
Two fundamental mathematical functions, the sine wave and the cosine wave, play critical roles in describing wave propagation.
The sine wave is often used as a basic building block to represent periodic waves. It describes a smooth, repetitive oscillation. In wave propagation, the sine wave describes how the displacement of a point in the medium varies over time and space as the wave passes.
The cosine wave is similar to the sine wave but is shifted by a phase of π/2. It also provides a smooth, oscillating representation of a wave. Together, sine and cosine waves can be combined to represent any complex wave pattern through Fourier analysis.
These waves can mathematically model and predict the behavior of waves as they propagate through various mediums. They help describe the wave’s amplitude, frequency, and phase.
Waves exhibit a fascinating interplay between spatial and temporal characteristics. We’ve established the crucial relationship between frequency and wavelength, highlighting how these properties define wave behavior. However, to fully quantify and understand wave phenomena, we must delve deeper into the wave equation itself and explore its connection to the period of a wave, alongside the energy it carries.
The Wave Equation and Period: Quantifying Wave Behavior
The wave equation is a fundamental tool in physics for describing the motion of waves. It elegantly connects a wave’s speed, frequency, and wavelength, providing a powerful means of predicting and analyzing wave behavior. Moreover, understanding the period of a wave – the time it takes for one complete cycle – adds another dimension to our understanding. This understanding allows us to quantify not only the wave’s spatial characteristics but also its temporal dynamics. Finally, we must consider the energy transported by a wave, a property directly related to its amplitude and frequency.
Deconstructing the Wave Equation
The wave equation, often expressed as v = fλ, provides a concise mathematical relationship between wave speed (v), frequency (f), and wavelength (λ). This equation is not merely a formula; it represents a fundamental principle governing all types of waves, from electromagnetic radiation to sound waves.
The equation dictates that the speed of a wave is directly proportional to both its frequency and its wavelength. In simpler terms, a wave with a higher frequency or a longer wavelength will travel faster, assuming the medium through which it propagates remains constant.
It’s important to recognize the implications of this relationship.
For example, if the speed of a wave remains constant, an increase in frequency will necessarily result in a decrease in wavelength, and vice-versa. This inverse relationship is a cornerstone of wave physics.
Time Period, Frequency, and Wavelength: An Intertwined Trinity
The period (T) of a wave is defined as the time required for one complete wave cycle to pass a given point. It is inversely related to the frequency (f), expressed as T = 1/f. This equation highlights a direct connection between the rate of oscillation and the time it takes for each oscillation to complete.
Furthermore, the period can be indirectly linked to the wavelength through the wave equation. Since v = fλ and T = 1/f, we can derive that λ = vT. This equation reveals that the wavelength is equal to the wave’s speed multiplied by its period.
Therefore, knowing any two of these three quantities—frequency, wavelength, or period—allows us to determine the third, given the wave speed. This interconnectedness underscores the fundamental unity of wave properties.
Wave Energy: The Amplitude Connection
The energy (E) carried by a wave is directly proportional to the square of its amplitude (A) and, in many cases, also related to its frequency (f). While the exact relationship varies depending on the type of wave, the general principle remains the same: larger amplitude and higher frequency waves carry more energy.
For example, in the case of electromagnetic waves, the energy is proportional to the frequency (E = hf, where h is Planck’s constant). This means that higher-frequency electromagnetic radiation, such as ultraviolet light or X-rays, carries significantly more energy than lower-frequency radiation, such as radio waves.
Similarly, for mechanical waves like sound waves, the energy is proportional to the square of the amplitude. A louder sound (higher amplitude) carries more energy than a quieter sound.
The amplitude, therefore, acts as a direct indicator of the energy being transported by the wave. This is why high-amplitude waves can be so powerful and potentially destructive, as they deposit a large amount of energy in a short amount of time.
Real-World Applications of Wavelength
Having dissected the fundamental properties of waves and their mathematical relationships, it’s time to appreciate their tangible impact on our daily lives. Wavelength, far from being an abstract concept, underpins a vast array of technologies and natural phenomena that shape our modern world. From the invisible signals that connect us to the intricate processes that allow us to see, understanding wavelength unlocks a deeper appreciation for the physics that governs our reality.
Communication Technologies: Riding the Waves of Information
The modern communication landscape relies heavily on the manipulation and transmission of electromagnetic waves. Radio, television, and mobile communication systems all leverage specific wavelengths to carry information across vast distances. The selection of a particular wavelength is not arbitrary; it’s a carefully calculated decision based on factors like atmospheric conditions, desired range, and bandwidth requirements.
For example, radio waves, with their longer wavelengths, can diffract around obstacles and travel farther, making them suitable for broadcasting signals across large geographical areas. Different radio frequencies are allocated for various uses, from AM and FM radio to shortwave broadcasts.
Television signals, also transmitted via radio waves, often utilize higher frequencies than AM radio to accommodate the broader bandwidth needed for video transmission.
Mobile communication employs microwaves, which offer a balance between wavelength and frequency, allowing for high data transfer rates while maintaining reasonable antenna sizes. The evolution of mobile technology from 2G to 5G has involved the exploration of increasingly higher frequencies and shorter wavelengths to support the growing demand for bandwidth-intensive applications.
The relationship between wavelength and frequency is crucial here. Recall that the shorter the wavelength, the higher the frequency, and the greater the amount of information that can be transmitted. This is why we are constantly pushing for technologies that operate at higher frequencies.
Medical Imaging: Peering Beneath the Surface
Wavelength also plays a critical role in various medical imaging techniques, enabling doctors to visualize the internal structures of the human body without invasive surgery. X-rays and Magnetic Resonance Imaging (MRI), while vastly different in their underlying physics, both rely on the interaction of electromagnetic waves with biological tissues.
X-rays, with their short wavelengths and high energy, can penetrate soft tissues but are absorbed by denser materials like bone. This differential absorption allows for the creation of images that reveal bone fractures, tumors, and other abnormalities.
The downside of X-rays is their ionizing radiation, which can potentially damage cells. Therefore, the exposure to X-rays is always kept to a minimum and carefully controlled.
MRI, on the other hand, uses strong magnetic fields and radio waves to generate images. The process involves aligning the magnetic moments of atomic nuclei within the body and then perturbing them with radio frequency pulses. The emitted signals are then processed to create detailed images of soft tissues, organs, and blood vessels. MRI is particularly useful for imaging the brain, spinal cord, and joints, where soft tissue contrast is essential.
Unlike X-rays, MRI does not involve ionizing radiation, making it a safer alternative for certain applications, especially in pregnant women and children.
Optics and Vision: A World Painted by Wavelengths
Our perception of color is directly linked to the wavelengths of light that reach our eyes. The visible light spectrum spans a narrow range of wavelengths, from approximately 400 nanometers (violet) to 700 nanometers (red). Different wavelengths within this range are perceived as different colors.
When white light, which is a mixture of all visible wavelengths, shines on an object, some wavelengths are absorbed, and others are reflected. The reflected wavelengths determine the color we perceive. For example, a red apple absorbs most wavelengths of light but reflects red wavelengths, which then enter our eyes and are interpreted by our brains as the color red.
The human eye contains specialized cells called cone cells that are sensitive to different ranges of wavelengths: short (blue), medium (green), and long (red). The relative activation of these cone cells allows us to perceive a vast array of colors. Color blindness occurs when one or more of these cone cell types are deficient or absent.
Furthermore, the wavelength of light also affects its interaction with optical elements like lenses and prisms. Shorter wavelengths of light are bent more than longer wavelengths when passing through a prism, resulting in the dispersion of white light into its constituent colors. This phenomenon is responsible for the formation of rainbows.
FAQs: Understanding Wavelengths
This section answers common questions about wavelengths, crests, and troughs, to help you better grasp these key concepts.
What exactly is a wavelength?
A wavelength is the distance between two identical points on a wave, such as from crest to crest or trough to trough. It’s a fundamental property used to describe waves of all types.
What are crests and troughs on a wave?
A crest is the highest point on a wave. Conversely, a trough is the lowest point on a wave. Understanding the distance between consecutive wavelength crest trough combinations helps determine the wave’s characteristics.
How does wavelength relate to energy?
Shorter wavelengths correspond to higher energy, and longer wavelengths correspond to lower energy. This relationship is crucial in understanding the electromagnetic spectrum and various forms of radiation.
Why is understanding the wavelength crest trough important?
Understanding wavelength, crests, and troughs is essential in fields like physics, engineering, and even medicine. These concepts explain wave behavior and how energy is transmitted through different media and are the key to many scientific applications.
So, there you have it! Hopefully, you now have a clearer picture of wavelength crest trough. Keep experimenting, keep questioning, and see how these wavelength crest trough concepts play out in the real world. Have fun!