Understanding projectile motion requires acknowledging gravity, the constant force influencing every trajectory and projectile. Newton’s Laws of Motion provide the foundational principles governing these paths, defining how forces affect acceleration. Ballistics, a specialized field, focuses specifically on calculating and predicting these trajectories, particularly relevant in fields like engineering and even sports like archery. Accurate prediction of trajectory and projectile requires careful analysis of initial velocity, launch angle, and environmental factors.
Optimizing Article Layout for "Master Trajectory & Projectile Motion: An Expert Guide"
The ideal article layout for "Master Trajectory & Projectile Motion: An Expert Guide," focusing on the keyword "trajectory and projectile," should be structured to progressively build understanding, starting from fundamental concepts and advancing to more complex applications. The primary goal is to ensure the information is easily digestible and accessible to a wide audience, regardless of their prior knowledge.
Understanding the Basics: What are Trajectory and Projectile Motion?
This section acts as the foundation. It defines key terms clearly and concisely.
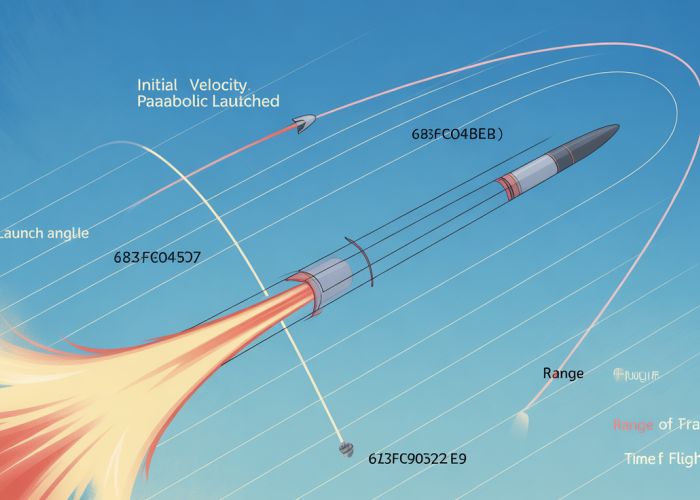
Defining "Trajectory"
- Trajectory is the path that an object follows as it moves through space. Think of a thrown ball or a rocket’s flight path. It’s crucial to emphasize that trajectory is a visual representation of motion.
- It’s a curve that shows how the object’s position changes over time.
- Consider including a simple diagram showing a curved path with labelled starting and ending points.
Defining "Projectile"
- A projectile is any object that is launched or thrown into the air and is only affected by gravity and air resistance (which we will initially ignore for simplicity).
- Examples of projectiles include baseballs, cannonballs, and even water droplets spraying from a hose.
- A projectile isn’t self-propelled during flight; its motion is determined by its initial conditions.
Introducing Projectile Motion
- Projectile motion describes the movement of a projectile under the influence of gravity.
- It combines horizontal and vertical motion. These motions are independent of each other, a crucial concept to explain.
- Use a short, engaging real-world example to illustrate (e.g., kicking a soccer ball).
Deconstructing Projectile Motion: The Two Dimensions
This section breaks down the components of projectile motion for easier understanding.
Horizontal Motion: Constant Velocity
- In an idealized scenario (no air resistance), the horizontal velocity of a projectile remains constant.
- Explain that this is due to the absence of horizontal forces acting on the projectile.
- Use the formula: Distance = Velocity x Time. Illustrate this with a simple example.
Vertical Motion: Accelerated Motion
- The vertical motion is governed by gravity, causing a constant downward acceleration (approximately 9.8 m/s²).
- Discuss the effect of gravity: it slows the upward motion, stops it momentarily at the peak, and then accelerates the downward motion.
- Emphasize the use of kinematic equations for vertical motion, such as:
v = u + at(final velocity = initial velocity + acceleration x time)s = ut + (1/2)at²(distance = initial velocity x time + (1/2) x acceleration x time²)
Independence of Horizontal and Vertical Motion
- This is a critical concept. Explain that the horizontal velocity does not affect the vertical acceleration, and vice-versa.
- Use an analogy: imagine dropping a ball straight down and simultaneously throwing another ball horizontally. They will both hit the ground at the same time (assuming they are released from the same height).
Key Factors Affecting Trajectory
This section explores the variables that influence the path of a projectile.
Initial Velocity: Speed and Angle
- The initial velocity (speed and direction) is the most important factor determining the trajectory.
- Explain the effect of initial speed: a faster initial speed results in a longer range.
- Discuss the effect of launch angle. An angle of 45 degrees theoretically yields the maximum range (in a vacuum). Use diagrams to illustrate different launch angles and their resulting trajectories.
The Role of Gravity
- Reiterate that gravity is the only force acting on the projectile (ideally) after it’s launched.
- Explain how gravity causes the projectile to accelerate downwards, resulting in a parabolic path.
Understanding Range, Height, and Time of Flight
- Define each of these terms clearly.
- Range: The horizontal distance covered by the projectile.
- Maximum Height: The highest vertical position reached by the projectile.
- Time of Flight: The total time the projectile spends in the air.
- Present formulas for each of these quantities, explaining their derivation and limitations.
Working Through Examples: Solving Projectile Motion Problems
This section provides practical applications of the concepts discussed.
Example 1: Simple Projectile Launched Horizontally
- A ball rolls off a table. Calculate the time it takes to hit the ground and the horizontal distance it travels.
- Show the step-by-step solution, clearly explaining the application of relevant formulas.
Example 2: Projectile Launched at an Angle
- A cannonball is fired at an angle of 30 degrees with an initial velocity of 50 m/s. Calculate its range, maximum height, and time of flight.
- Again, provide a detailed solution, breaking down each step.
Example 3: Considering Air Resistance (Qualitative)
- Discuss, qualitatively, how air resistance affects the trajectory.
- Explain that air resistance reduces the range, maximum height, and time of flight. It also makes the trajectory non-parabolic.
- Mention that calculating projectile motion with air resistance requires more advanced techniques and is beyond the scope of this introductory guide.
Advanced Topics in Trajectory and Projectile Motion (Optional)
This section introduces more complex considerations for those seeking deeper knowledge.
Spin and the Magnus Effect
- Briefly explain how spin affects the trajectory of a projectile (e.g., a baseball).
- Introduce the Magnus effect: the force exerted on a spinning object moving through a fluid (air or water).
The Coriolis Effect
- Explain how the Earth’s rotation affects projectile motion over long distances.
- Give examples such as long-range artillery or weather patterns.
Trajectory Optimization
- Briefly mention how trajectories can be optimized for various purposes, such as maximizing range or minimizing time.
Table of Equations
Provide a table summarizing all the key equations used throughout the article. For example:
| Equation | Description | Variables |
|---|---|---|
v = u + at |
Final velocity | v = final velocity, u = initial velocity, a = acceleration, t = time |
s = ut + (1/2)at² |
Distance traveled | s = distance, u = initial velocity, a = acceleration, t = time |
Range = (v² sin(2θ)) / g |
Range of a projectile (without air resistance) | v = initial velocity, θ = launch angle, g = acceleration due to gravity |
This layout ensures a comprehensive and digestible explanation of trajectory and projectile motion, addressing the topic from fundamental principles to more advanced concepts. The progressive structure allows readers to build their understanding step-by-step, making the guide accessible and informative for a broad audience.
FAQs About Mastering Trajectory and Projectile Motion
Hopefully, the article cleared up some questions about trajectory and projectile motion. Here are some common questions we get that will hopefully help further.
What’s the key difference between trajectory and projectile motion?
Trajectory refers to the path an object follows through space. Projectile motion, however, describes the physics governing that movement. It’s influenced by gravity and initial velocity.
In essence, trajectory is what you see, and projectile motion explains why the object moves that way.
Does air resistance always affect a projectile’s trajectory?
In theory, yes. Air resistance is always present to some degree. However, in simplified calculations of projectile motion, air resistance is often ignored to make the problem easier to solve.
For real-world applications, particularly when dealing with high speeds or light objects, air resistance becomes a significant factor in determining the projectile’s trajectory.
What’s the optimal launch angle for maximum range of a projectile?
Ignoring air resistance, the optimal launch angle for maximizing the horizontal range of a projectile is 45 degrees. This angle provides the best balance between initial horizontal and vertical velocity components.
However, with air resistance, the optimal angle is often slightly less than 45 degrees. It depends on the projectile’s shape, mass, and initial velocity.
How does gravity impact the vertical velocity of a projectile during its trajectory?
Gravity causes a constant downward acceleration on the projectile. This means that the projectile’s upward velocity decreases as it rises, momentarily becoming zero at the peak of its trajectory.
Then, the projectile’s downward velocity increases at a constant rate due to gravity, until it hits the ground. Gravity is the primary force shaping the vertical component of projectile motion.
So, feeling a bit more confident navigating the world of trajectory and projectile? Awesome! Now go out there and apply what you’ve learned. Let me know if you have any questions, and good luck with your projects!