Unlock Ellipses! Key Properties You Need to Know Now

Geometry, a branch of mathematics, provides the framework for understanding shapes like ellipses, which exhibit unique properties of ellipses. NASA, an organization dedicated to space exploration, frequently utilizes the geometric properties of ellipses in orbital mechanics. The eccentricity of an ellipse, a fundamental characteristic, quantifies its deviation from a perfect circle. Calculus provides the tools to precisely analyze the areas and perimeters of ellipses, enabling advanced calculations. Kepler’s laws of planetary motion, based on astronomical observations, famously describe the elliptical paths of planets around stars.

The ellipse, a captivating cousin of the circle, graces our world with its unique form.

It’s a shape often overlooked, yet it plays a crucial role in phenomena ranging from the celestial dance of planets to the very structures we inhabit.

Unlike the perfect symmetry of a circle, the ellipse possesses a subtle elongation, an asymmetry that lends it both beauty and functionality.

This article embarks on a journey to explore this fascinating geometric figure, revealing its underlying principles and its far-reaching implications.

A Fundamental Geometric Shape

At its core, the ellipse is a fundamental geometric shape, defined by a specific set of rules.

It’s a closed curve, much like a circle, but instead of a single center point, it is governed by two focal points.

The relationship between these foci dictates the ellipse’s unique form, creating a spectrum of shapes from nearly circular to highly elongated.

Capturing Interest: Real-World Applications

The ellipse isn’t confined to textbooks and theoretical calculations. It manifests itself in the real world in a multitude of ways:

• Astronomy: Perhaps the most well-known application is in the realm of astronomy. Planets, comets, and asteroids all trace elliptical paths around stars, governed by the laws of gravity. These elliptical orbits are a testament to the fundamental nature of this shape in the cosmos.

• Architecture: Architects and designers have long appreciated the aesthetic and structural properties of the ellipse. Elliptical arches and domes offer a pleasing visual appeal while distributing weight effectively. Many famous structures incorporate elliptical designs to achieve both beauty and structural integrity.

• Whispering Galleries: Elliptical rooms, known as whispering galleries, demonstrate the unique acoustic properties of the shape. A whisper at one focus can be clearly heard at the other, even across a significant distance. This phenomenon showcases the ellipse’s ability to focus sound waves.

Thesis Statement: Understanding the Ellipse

This article aims to provide a comprehensive understanding of the ellipse, dissecting its key properties and revealing its significance in various fields.

We will explore the mathematical foundations, the geometric relationships, and the practical applications that make the ellipse such a compelling and important shape.

By the end of this exploration, you will have a deeper appreciation for the elegance and utility of the ellipse in the world around us.

The ellipse isn’t confined to textbooks and theoretical calculations. It manifests itself in the real world in a multitude of ways. From the grand scale of astronomy to the more intimate designs of architecture, the ellipse demonstrates its versatility. To truly appreciate its widespread relevance, a firm understanding of its fundamental properties is essential.

Defining the Ellipse: A Geometric Perspective

At its heart, the ellipse is a geometric marvel, a shape defined not by a single center like a circle, but by a unique relationship between two crucial points. Understanding this relationship unlocks the secrets to the ellipse’s form and behavior.

The Locus Definition: Tracing the Ellipse

The most formal way to define an ellipse is through the concept of a locus. An ellipse is the locus of all points in a plane where the sum of the distances from each point to two fixed points remains constant.

Think of it like this: imagine two thumbtacks (the foci) pinned to a board. Now, take a length of string longer than the distance between the thumbtacks. Tie the ends of the string to the thumbtacks. If you hold a pencil against the string, keeping it taut, and trace around the thumbtacks, you’ll draw an ellipse.

The length of the string represents the constant sum of distances, and the path the pencil traces is the ellipse itself. This "string and pins" analogy vividly illustrates the fundamental definition.

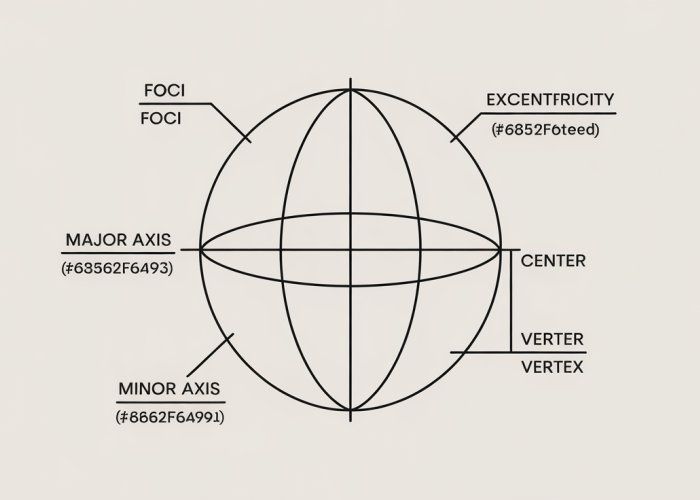
Foci (Focuses): The Cornerstone of the Ellipse

The two fixed points that govern the ellipse’s shape are called the foci (singular: focus). They are the cornerstone of the ellipse, dictating its elongation and orientation.

The Role of Foci in Shaping the Ellipse

The position of the foci drastically impacts the ellipse’s appearance. If the foci are close together, the ellipse resembles a circle. As the foci move further apart, the ellipse becomes increasingly elongated, transforming into a more stretched-out oval.

In the extreme case, if the two foci coincide, the ellipse becomes a perfect circle. Conversely, as the distance between the foci approaches the constant sum of distances, the ellipse becomes increasingly narrow.

The Constant Sum: Linking Foci and Shape

The relationship between the foci and the constant sum of distances is key to understanding the ellipse. The closer the foci are to each other relative to the constant sum, the more circular the ellipse becomes. The further apart they are, the more elongated.

This constant sum dictates the size of the ellipse; a larger sum results in a larger ellipse, while a smaller sum creates a smaller one. The foci position determines its proportions. The interplay between these two factors – the foci and the constant sum – gives the ellipse its distinctive and versatile form.

The foci provide the foundational points for defining the ellipse, but they aren’t the only critical elements shaping its form. Beyond these points lie lines and additional points that contribute significantly to understanding and working with ellipses. These are the axes, the center, and the vertices, each holding a distinct place in the ellipse’s geometry.

Key Components: Axes, Center, and Vertices

The ellipse isn’t just a random oval; it’s a precisely defined shape with key components that dictate its size, orientation, and overall appearance. Among the most important are its axes, its center point, and the locations of its vertices and co-vertices.

Major Axis and Minor Axis: The Principal Axes

Ellipses, unlike circles, have two axes of symmetry: the major axis and the minor axis. These axes are perpendicular to each other and intersect at the center of the ellipse.

The major axis is the longer of the two axes. It passes through both foci and the center of the ellipse. It represents the maximum width of the ellipse. The length of the major axis is often denoted as 2a.

The significance of the major axis lies in its direct relationship to the foci. It defines the direction in which the ellipse is "stretched" and plays a crucial role in determining the shape’s eccentricity.

The minor axis, conversely, is the shorter axis of the ellipse. It is perpendicular to the major axis and also passes through the center. It represents the minimum width of the ellipse. The length of the minor axis is often denoted as 2b.

The significance of the minor axis is that it constrains the ellipse’s shape in the direction perpendicular to the major axis. Its length, in relation to the major axis, dictates how "squashed" or circular the ellipse appears.

Center: The Ellipse’s Midpoint

The center of the ellipse is the midpoint of both the major and minor axes. It’s the point where the two axes intersect and represents the geometric center of the shape.

If you were to rotate the ellipse 180 degrees around its center, the ellipse would remain unchanged. This symmetry makes the center a natural point of reference for describing and analyzing the ellipse.

In the standard equation of an ellipse, the center’s coordinates are denoted as (h, k). These coordinates are essential when defining the ellipse’s position in a coordinate plane.

Vertices and Co-vertices: The Endpoints of the Axes

The vertices and co-vertices are the endpoints of the major and minor axes, respectively.

The vertices are the two points where the major axis intersects the ellipse. They are the points farthest from the center along the major axis. Understanding where the vertices are located helps define the overall size and orientation of the ellipse.

The co-vertices are the two points where the minor axis intersects the ellipse. They are the points closest to the center along the minor axis. They help define the "width" of the ellipse perpendicular to the major axis.

The vertices and co-vertices, along with the center, provide a framework for sketching the ellipse accurately and for determining its key dimensions. These points are particularly useful when graphing ellipses or working with their equations.

The major and minor axes provide a clear indication of an ellipse’s overall dimensions, but to truly grasp its unique shape, we need to delve into measurements that describe its curvature and “ovalness.” This is where the concepts of semi-axes and eccentricity come into play, offering a more refined understanding of the ellipse’s geometry.

Quantifying Ovalness: Semi-Axes and Eccentricity

Semi-Major Axis and Semi-Minor Axis: Halving the Axes

The semi-major axis and semi-minor axis are, quite simply, half the lengths of the major and minor axes, respectively.

If we denote the length of the major axis as 2a, then the semi-major axis is a. Similarly, if the length of the minor axis is 2b, the semi-minor axis is b.

These values, a and b, are fundamental in defining the ellipse and appear prominently in its equation. They represent the distances from the center of the ellipse to the vertices and co-vertices, respectively.

The semi-major axis, a, is always greater than or equal to the semi-minor axis, b. In the special case where a = b, the ellipse becomes a circle.

Eccentricity: Quantifying the "Ovalness"

While the semi-axes define the size of the ellipse, eccentricity (denoted by e) is a dimensionless number that quantifies its shape – specifically, how much it deviates from being a perfect circle.

Eccentricity is defined as the ratio of the distance between the foci (c) and the length of the semi-major axis (a):

e = c / a

Where c is the distance from the center of the ellipse to each focus, and a is the length of the semi-major axis.

The Range of Eccentricity: From Circle to Line

The value of eccentricity always lies between 0 and 1 (0 ≤ e < 1). This range directly corresponds to the shape of the ellipse:

• e = 0: The ellipse is a circle. In this case, the foci coincide at the center, and the major and minor axes are equal.
• As e approaches 1: The ellipse becomes increasingly elongated, approaching a line segment. The foci move closer to the vertices.

Eccentricity and the Shape of the Ellipse

A low eccentricity (close to 0) signifies an ellipse that is nearly circular. The closer the eccentricity is to 0, the more the ellipse resembles a circle.

Conversely, a high eccentricity (close to 1) indicates a highly elongated ellipse. The ellipse is stretched out, and the foci are located closer to the ends of the ellipse.

Understanding eccentricity provides a powerful way to compare different ellipses and visualize their shapes.

By knowing just the eccentricity and the semi-major axis, one can fully characterize the geometry of any ellipse. It’s a single number that encapsulates the essence of its "ovalness."

Eccentricity gives us a sense of an ellipse’s shape, capturing its deviation from circularity. But to fully wield the power of ellipses, we need a language to describe them precisely: the language of mathematics. The equation of an ellipse provides a concise and powerful way to represent its properties and perform calculations.

The Equation of an Ellipse: A Mathematical Representation

The equation of an ellipse isn’t just a jumble of symbols; it’s a blueprint that encodes all of the ellipse’s essential characteristics. By understanding its structure, we can unlock key information about the ellipse’s size, shape, and orientation. Let’s explore the standard forms of the equation and how to interpret them.

Standard Form with Center at the Origin

The simplest form of the ellipse equation arises when the ellipse is centered at the origin (0, 0) of the Cartesian coordinate system. In this case, the equation takes one of two forms, depending on whether the major axis is horizontal or vertical:

• Horizontal Major Axis: (x² / a²) + (y² / b²) = 1

• Vertical Major Axis: (x² / b²) + (y² / a²) = 1

In both equations, a represents the length of the semi-major axis and b represents the length of the semi-minor axis. The key difference is that a always corresponds to the variable associated with the major axis.

Notice how the equation elegantly captures the relationship between x and y coordinates on the ellipse, constrained by the semi-major and semi-minor axes. If a = b, both become radii resulting in (x² / a²) + (y² / a²) = 1 which is x² + y² = a², the familiar equation of a circle.

Standard Form with Center at (h, k)

What happens when the ellipse isn’t conveniently centered at the origin? We simply introduce horizontal and vertical shifts, represented by the coordinates (h, k) of the center. The equation then becomes:

• Horizontal Major Axis: ((x – h)² / a²) + ((y – k)² / b²) = 1

• Vertical Major Axis: ((x – h)² / b²) + ((y – k)² / a²) = 1

The (x – h) and (y – k) terms effectively translate the ellipse so that its center is located at the point (h, k) instead of (0, 0).

This more general form allows us to describe any ellipse, regardless of its position in the coordinate plane.

Extracting Key Properties from the Equation

The power of the ellipse equation lies in our ability to extract meaningful information from it. By carefully examining the equation, we can determine the ellipse’s center, the lengths of its axes, and the location of its foci.

Finding the Center, Semi-Axes, and Orientation

The coordinates (h, k) directly reveal the center of the ellipse.

The values a and b, found in the denominators, give us the lengths of the semi-major and semi-minor axes, respectively. Remember that a is always associated with the major axis.

By observing which variable (x or y) has a in its denominator, we can determine whether the major axis is horizontal or vertical.

Locating the Foci

To find the foci, we need to calculate the distance c from the center to each focus. This is found using the equation:

c² = a² – b²

Once we have c, the foci are located along the major axis, c units away from the center.

• Horizontal Major Axis: Foci are at (h ± c, k)

• Vertical Major Axis: Foci are at (h, k ± c)

The ellipse’s equation is more than just a formula; it’s a gateway to understanding its geometry and properties. By mastering the equation and its interpretations, we can confidently analyze and manipulate ellipses in various mathematical and scientific contexts.

Ellipses in Action: From Astronomy to Orbits

Having armed ourselves with the mathematical tools to describe ellipses, it’s time to witness these elegant curves in action. From the grand scale of celestial mechanics to the intricacies of engineering, ellipses manifest in surprising and impactful ways. Perhaps nowhere is their influence more profoundly felt than in the realm of astronomy, where they dictate the very paths of planets and shape our understanding of the cosmos.

Johannes Kepler and Elliptical Orbits

Johannes Kepler, a 17th-century astronomer, revolutionized our understanding of planetary motion. Prior to Kepler, the prevailing belief, inherited from the Greeks, was that planets moved in perfect circles around the Sun. Kepler, through meticulous analysis of observational data collected by Tycho Brahe, shattered this paradigm.

Kepler’s First Law: The Law of Ellipses

Kepler’s First Law of Planetary Motion, often referred to as the Law of Ellipses, states that each planet orbits the Sun in an ellipse, with the Sun at one focus.

This seemingly simple statement had profound implications.

It meant that planetary orbits are not perfect circles, but rather ellipses characterized by a certain degree of eccentricity. It also meant that a planet’s distance from the Sun varies throughout its orbit. This variance, in turn, affects the planet’s speed, as dictated by Kepler’s Second Law (though outside our scope here).

Orbital Mechanics and Elliptical Paths

The elliptical nature of orbits isn’t just a quirk of planetary motion; it’s a fundamental consequence of the laws of gravity. Understanding why orbits are elliptical requires delving into the realm of orbital mechanics.

Why Not Circular?

Why don’t planets orbit in perfect circles? The answer lies in the initial conditions that set the planets in motion billions of years ago and conservation laws of physics. For a perfectly circular orbit to occur, a planet would need a very specific velocity and direction relative to the star. Even small deviations from these precise conditions will result in an elliptical orbit.

Moreover, gravitational interactions with other celestial bodies can perturb orbits, nudging them away from perfect circularity. These perturbations are common in our solar system.

The Role of Focal Points

The location of the focal points of an elliptical orbit has significant consequences for the orbiting body. As Kepler’s First Law states, the central star (e.g., the Sun) resides at one focus of the ellipse. This arrangement dictates the points of closest approach (perihelion) and farthest distance (aphelion) in the orbit.

The distance between the focal points influences the eccentricity of the ellipse, and thus the severity of the difference between perihelion and aphelion distances. Planets experience stronger gravitational forces, and thus move faster, when they are closer to the star at perihelion.

So, that’s the lowdown on properties of ellipses! Hopefully, you found something useful in there. Now go forth and ellipse!