The relationship between period from frequency and oscillatory phenomena is fundamental in fields like electrical engineering. Understanding how to accurately determine period from frequency is crucial, especially when dealing with complex circuits at institutions such as the National Institute of Standards and Technology (NIST), where precision is paramount. Furthermore, tools like the oscilloscope play a vital role in visualizing and measuring these properties, enabling engineers and researchers, including individuals like Nikola Tesla (a pioneer in alternating current) to effectively analyze and manipulate waveforms. Mastering the concept of period from frequency, therefore, unlocks deeper insights into a range of scientific and engineering applications.

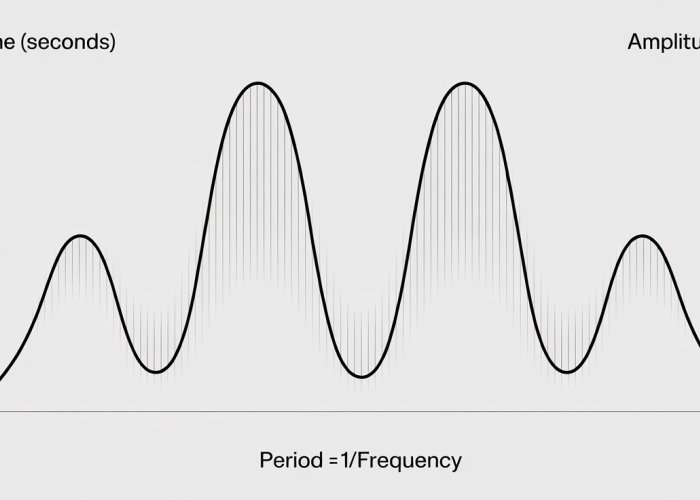
The world around us pulses with rhythmic events, from the subtle blink of an eye to the soaring notes of a musical masterpiece. These seemingly disparate phenomena are united by two fundamental concepts: period and frequency. Understanding their intricate relationship is key to unlocking the secrets of countless natural and technological processes.

The Blink of an Eye: A Relatable Rhythm

Consider something as simple as blinking. The rate at which we blink, or how often we blink per minute, describes a frequency. The duration of each blink cycle, from the moment the eyelid closes to when it reopens, defines a period. This simple example illustrates the core principle: frequency and period are inextricably linked, acting as two sides of the same coin.

Defining Frequency and Period in Wave Physics

In the realm of physics, particularly when studying waves, frequency refers to the number of complete cycles of a wave that occur per unit of time. It is typically measured in Hertz (Hz), where 1 Hz represents one cycle per second. Think of a buoy bobbing up and down on the ocean’s surface. The number of times it completes a full up-and-down motion in one second is the wave’s frequency.

Period, on the other hand, is the time it takes for one complete cycle of a wave to occur. Measured in seconds, the period represents the duration of a single oscillation. In the buoy example, the period is the time it takes for the buoy to return to its starting position after bobbing up and down.

The Significance of Understanding the Relationship

The inverse relationship between period and frequency is not merely a mathematical curiosity. It is a fundamental principle that governs a vast array of applications, from telecommunications to medical imaging.

By understanding how period and frequency relate, we can effectively analyze and manipulate these rhythmic phenomena. This understanding allows us to design efficient communication systems, interpret medical data with greater accuracy, and even appreciate the nuances of music and sound.

Therefore, grasping the relationship between period and frequency is paramount for anyone seeking to delve deeper into the workings of the physical world. This foundational knowledge serves as a stepping stone for exploring more complex concepts in science and engineering, enabling us to decipher the rhythms that shape our universe.

The buoy’s rhythmic dance highlights the dynamic interplay of period and frequency. But how do we quantify this relationship? How can we move beyond mere observation and delve into the precise mathematical connection that governs these concepts?

The Fundamental Formula: Demystifying the Equation

At the heart of the relationship between period and frequency lies a simple, yet powerful equation. Understanding this formula is paramount to mastering these concepts.

The Core Formula: Period (T) = 1 / Frequency (f)

The relationship between period and frequency is inversely proportional. This means that as frequency increases, the period decreases, and vice versa.

Mathematically, this is expressed as:

T = 1 / f

Where:

• T represents the period, which is the time taken for one complete cycle.
• f represents the frequency, which is the number of cycles per unit of time.

This equation elegantly captures the essence of their interconnectedness. If you know the frequency of an event, you can readily calculate its period, and conversely, if you know the period, you can determine its frequency.

Importance of Units of Measurement

The correct units of measurement are critical when working with the period and frequency formula. Using the wrong units will lead to incorrect calculations and a misunderstanding of the results.

• Frequency: Frequency is typically measured in Hertz (Hz). One Hertz is defined as one cycle per second. For higher frequencies, you might encounter kilohertz (kHz), megahertz (MHz), or gigahertz (GHz).

• Period: Period is measured in units of time, usually seconds (s). However, depending on the context, it can also be expressed in milliseconds (ms), microseconds (µs), or even minutes or hours.

It is crucial to ensure that the units are consistent before performing any calculations. If frequency is given in kHz, it must be converted to Hz before using the formula if the period is to be calculated in seconds.

Real-World Examples

Let’s solidify our understanding with a few practical examples.

Example 1: A Pendulum’s Swing

Imagine a pendulum that completes one full swing (back and forth) every 2 seconds.
The period (T) of the pendulum is 2 seconds.
To find the frequency (f), we use the formula:

f = 1 / T = 1 / 2 seconds = 0.5 Hz

This means the pendulum oscillates at a frequency of 0.5 cycles per second.

Example 2: Radio Waves

A radio station broadcasts at a frequency of 100 MHz (100 million Hertz).
To find the period (T) of the radio wave, we use the formula:

T = 1 / f = 1 / 100,000,000 Hz = 0.00000001 seconds = 10 nanoseconds

This incredibly short period reflects the high frequency of radio waves, demonstrating how quickly these waves oscillate.

Example 3: The Heart’s Rhythm

A healthy heart beats approximately 60 times per minute.
To find the frequency in Hertz, we first convert beats per minute to beats per second:

60 beats/minute / 60 seconds/minute = 1 beat/second = 1 Hz

Therefore, the period (T) of a heartbeat is:

T = 1 / f = 1 / 1 Hz = 1 second

These examples illustrate the versatility of the formula and its applicability across diverse scenarios. By understanding the relationship and paying close attention to units, you can confidently navigate the world of period and frequency.

The formula provides the mathematical framework, but to truly grasp the essence of period and frequency, we must delve into the fundamental concepts that underpin them. Understanding oscillation, cycles, and the crucial role of time provides a richer and more intuitive understanding.

Diving Deeper: Understanding the Concepts

Oscillation, Cycles, and the Dance of Repetition

At its core, frequency relates to how often something oscillates or repeats a complete sequence of movements or values.

Think of a pendulum swinging back and forth, a spring bouncing up and down, or even the alternating current in your home’s electrical wiring.

Each complete swing, bounce, or directional change represents a cycle.

Defining the Cycle

A cycle is a single, complete iteration of a repeating event.

For a wave, a cycle extends from one peak (or trough) to the next identical peak (or trough).

The period measures the time it takes to complete this single cycle, while frequency counts how many of these cycles occur within a given unit of time (usually a second).

Therefore, a high frequency indicates rapid oscillations and short periods, while a low frequency suggests slow oscillations and longer periods.

The connection between oscillation and cycle is thus fundamental: oscillation is the act of repetitive motion, and a cycle is one complete unit of that motion.

Frequency measures the rate of these cycles, and the period measures their duration.

Time as the Bedrock of Periodicity

Time is the indispensable foundation upon which both period and frequency are built.

The period, by definition, is a measure of time – specifically, the time required for one complete cycle of an oscillating system.

Without the concept of time, we couldn’t quantify how long an event lasts or how frequently it repeats.

Consider a simple example: a heartbeat.

If a person’s heart beats 60 times per minute, the frequency is 1 Hz (one cycle per second), and the period is 1 second (the time for one heartbeat).

The period provides a tangible measure of the duration of each heartbeat, emphasizing time as the fundamental element.

Similarly, in wave phenomena, the period represents the time it takes for one complete wavelength to pass a given point.

This highlights that understanding time is critical to understanding the period and frequency.

Period, Frequency, Wavelength, and Wave Speed

While period and frequency focus on the temporal aspects of a wave, wavelength describes its spatial extent.

Wavelength (λ) is the distance between two successive crests or troughs of a wave.

The relationship between wave speed (v), frequency (f), and wavelength (λ) is given by the equation:

v = fλ

This equation reveals that wave speed is directly proportional to both frequency and wavelength.

For a given wave speed, if the frequency increases, the wavelength decreases, and vice versa.

This interconnection further enriches our understanding of wave behavior.

While a comprehensive discussion is beyond our current scope, recognizing the interplay between period, frequency, wavelength, and wave speed provides a more holistic view of wave phenomena.

Time provides the bedrock upon which period and frequency exist, but their true power lies in their ability to explain and control a vast range of phenomena across diverse fields. From the invisible waves carrying our phone calls to the precisely timed vibrations creating music, period and frequency are not just abstract concepts; they are the fundamental tools we use to shape our world.

Practical Applications Across Disciplines

The beauty of period and frequency lies in their universality. These concepts are not confined to the physics classroom; they are essential tools used by engineers, musicians, doctors, and countless other professionals. Understanding how period and frequency manifest in different fields provides a deeper appreciation for their power and relevance.

Telecommunications: The Language of Waves

Telecommunications relies heavily on manipulating the frequency and period of electromagnetic waves. Radio waves, microwaves, and other forms of electromagnetic radiation are used to transmit information across vast distances.

The frequency of a wave determines its channel, allowing multiple signals to be transmitted simultaneously without interference. Think of radio stations; each station broadcasts at a unique frequency, allowing your radio to tune into the desired signal.

Modulation techniques, such as amplitude modulation (AM) and frequency modulation (FM), alter the characteristics of these waves to encode information. The period, or the time it takes for a wave to complete a cycle, is directly related to the amount of data that can be transmitted per unit of time.

Higher frequencies allow for faster data transfer rates. This is why newer technologies like 5G utilize much higher frequencies than older technologies.

Music and Sound: A Symphony of Frequencies

In the world of music, frequency is synonymous with pitch. The higher the frequency of a sound wave, the higher the perceived pitch.

Each musical note corresponds to a specific frequency; for example, the A above middle C is typically tuned to 440 Hz.

Musical instruments create sound waves with specific frequencies and periods. The interplay of these frequencies creates harmonies and melodies.

The period of a sound wave determines its duration. Shorter periods correspond to faster notes, while longer periods correspond to slower notes. Understanding the relationship between frequency, period, and pitch is essential for musicians, sound engineers, and anyone interested in the science of sound.

Medical Imaging: Seeing the Unseen

Medical imaging techniques, such as ultrasound, utilize the properties of frequency to create images of the inside of the human body.

Ultrasound uses high-frequency sound waves to penetrate tissue. The way these waves reflect back provides information about the density and structure of internal organs.

The frequency of the ultrasound waves affects the resolution and penetration depth of the image. Higher frequencies provide better resolution but penetrate less deeply, while lower frequencies penetrate deeper but offer lower resolution.

By carefully selecting the frequency of the ultrasound waves, medical professionals can obtain detailed images of various tissues and organs, aiding in diagnosis and treatment.

Other Applications: A Universe of Possibilities

The applications of period and frequency extend far beyond telecommunications, music, and medicine. In electrical engineering, they are crucial for designing and analyzing circuits.

In seismology, they are used to study the earthquakes and seismic waves, helping scientists understand the structure and dynamics of the Earth’s interior.

In astronomy, they are used to study the periodic variations in the brightness of stars, providing insights into their physical properties and evolution.

From the rhythmic ticking of a clock to the vast cycles of the cosmos, period and frequency are fundamental concepts that underpin our understanding of the world around us.

Telecommunications relies heavily on manipulating the frequency and period of electromagnetic waves. Radio waves, microwaves, and other forms of electromagnetic radiation are used to transmit information across vast distances.

Higher frequencies allow for faster data transfer rates. This is why, to truly grasp the power of period and frequency, one must learn to wield them. The ability to calculate and manipulate these values is paramount to applying them effectively in real-world scenarios.

Tools and Techniques for Calculation

Calculating period and frequency is not merely an academic exercise; it is a practical skill with applications spanning countless fields. Whether you’re an engineer designing circuits, a musician tuning an instrument, or a technician troubleshooting equipment, understanding how to calculate these values is essential. Fortunately, a range of tools and techniques are available to simplify the process, from manual calculations to sophisticated software solutions.

Manual Calculation: The Foundation of Understanding

Before relying on calculators and software, it’s crucial to understand the fundamental principles behind the calculations. This foundational knowledge empowers you to interpret results critically and avoid common errors.

The core formulas, as previously established, are:

• Period (T) = 1 / Frequency (f)
• Frequency (f) = 1 / Period (T)

These simple equations form the basis for all period and frequency calculations.

Step-by-Step Guide

Let’s illustrate with a practical example. Imagine a pendulum swings with a frequency of 0.5 Hz. To calculate the period of one complete swing:

1. Identify the known value: Frequency (f) = 0.5 Hz.
2. Apply the formula: Period (T) = 1 / f.
3. Substitute the value: T = 1 / 0.5.
4. Calculate the result: T = 2 seconds.

Therefore, the period of the pendulum’s swing is 2 seconds. The reverse calculation is equally straightforward. If you know the period is 2 seconds, the frequency is simply 1 / 2 = 0.5 Hz.

Importance of Practice

Mastering manual calculations requires practice. Work through various examples with different values to solidify your understanding. This will not only improve your calculation skills but also deepen your intuitive grasp of the inverse relationship between period and frequency.

Utilizing Online Period/Frequency Calculators

While manual calculations provide a solid foundation, online calculators offer speed and convenience, especially when dealing with complex numbers or repetitive calculations. Numerous free and reliable online tools are readily available.

Benefits of Online Calculators

• Speed and Efficiency: Quickly perform calculations without manual effort.
• Accuracy: Reduce the risk of human error, especially with complex numbers.
• Accessibility: Available on various devices with internet access.
• Unit Conversion: Some calculators offer built-in unit conversion features.

Choosing the Right Calculator

When selecting an online calculator, consider the following:

• Reputation: Opt for reputable websites with positive reviews.
• Accuracy: Verify the calculator’s accuracy by comparing its results with manual calculations.
• Features: Choose a calculator that meets your specific needs, such as unit conversion or scientific notation.

It is crucial to remember that online calculators should be used as tools to augment, not replace, your understanding of the underlying principles.

Applying Formulas in Spreadsheets or Programming Environments

For advanced users or those who require automated calculations, spreadsheets (like Excel or Google Sheets) and programming environments (like Python or MATLAB) offer powerful solutions.

Spreadsheets for Automated Calculations

Spreadsheets allow you to create custom calculators using formulas. You can input period or frequency values into designated cells, and the spreadsheet will automatically calculate the corresponding value using the 1/x formula.

This approach is particularly useful for:

• Batch Processing: Performing calculations on large datasets.
• Data Analysis: Integrating period and frequency calculations into larger analytical models.
• Visualization: Creating graphs and charts to visualize the relationship between period and frequency.

Programming for Complex Scenarios

Programming environments provide even greater flexibility and control. You can write scripts to perform complex calculations, simulate physical systems, and develop custom tools tailored to your specific needs.

For example, in Python, the following code snippet calculates the period from a given frequency:

def calculate_period(frequency):
"""Calculates the period from a given frequency.

Args:
frequency: The frequency in Hertz (Hz).

Returns:
The period in seconds, or None if the frequency is zero.
"""
if frequency == 0:
return None # Avoid division by zero
period = 1 / frequency
return period

Example usage

frequency = 10 # Hz
period = calculate_period(frequency)
print(f"The period for a frequency of {frequency} Hz is {period} seconds")

This level of automation is invaluable in research, engineering, and other fields where precise and efficient calculations are paramount. By mastering these tools and techniques, you unlock the full potential of period and frequency, transforming them from abstract concepts into powerful instruments for understanding and manipulating the world around you.

Common Pitfalls and How to Avoid Them

The power of period and frequency lies not just in their definition, but in their accurate application. Mastering these concepts demands diligence in avoiding common errors that can undermine calculations and lead to flawed conclusions.

Let’s examine some typical pitfalls and strategies to navigate them effectively.

The Perils of Unit Conversion

Perhaps the most frequent source of error in period and frequency calculations stems from inconsistent units. The standard unit for frequency is Hertz (Hz), representing cycles per second, while period is measured in seconds. However, real-world scenarios often present values in different units, such as milliseconds, kilohertz, or megahertz.

Failing to convert these values to their base units before performing calculations inevitably leads to incorrect results.

Maintaining Consistency

The key to avoiding unit conversion errors is meticulous attention to detail. Always double-check the units provided and ensure they align with the expected units in the formula.

When necessary, perform the appropriate conversions before plugging values into equations. For instance, if frequency is given in kHz, divide by 1000 to obtain Hz.

Similarly, if the period is in milliseconds, divide by 1000 to get seconds.

Creating a conversion table or using online unit converters can be helpful, but understanding the underlying principles is crucial for spotting errors.

Navigating the Inverse Relationship

The inverse relationship between period and frequency, while conceptually simple, can be a source of confusion if not carefully considered. It’s tempting to instinctively multiply instead of divide or to invert the values incorrectly.

A clear understanding of what each variable represents is paramount.

Conceptual Clarity

Remember that frequency tells you how many cycles occur in a given second. Period, on the other hand, tells you how long it takes for one complete cycle to occur.

This distinction is crucial. If you increase the frequency, you inherently decrease the time it takes for one cycle (the period), and vice versa.

To solidify this understanding, consider extreme examples.

A very high frequency implies a very short period, while a very low frequency implies a very long period. This simple check can help prevent errors arising from misinterpreting the inverse relationship.

Frequency vs. Angular Frequency

While frequency (f) measures cycles per second (Hz), angular frequency (ω) measures the rate of change of an angle, typically expressed in radians per second (rad/s). Although related, they are distinct concepts often confused.

Angular frequency is particularly relevant in contexts involving rotational motion or sinusoidal functions.

Understanding the Distinction

The relationship between frequency (f) and angular frequency (ω) is given by the formula:

ω = 2πf

This equation highlights that angular frequency is simply frequency multiplied by 2π, representing a full circle in radians.

The key is recognizing when to use each concept. Use frequency (f) when dealing with cycles per unit time. Use angular frequency (ω) when dealing with angular displacement per unit time.

Failing to distinguish between these concepts can lead to errors, particularly in calculations involving sinusoidal functions or rotational dynamics. Always clarify the context and the meaning of the values being used.

By understanding and actively addressing these common pitfalls, practitioners can wield the power of period and frequency with confidence. Meticulous attention to detail, a clear grasp of the underlying concepts, and a healthy dose of skepticism are the best defenses against errors in this domain.

Advanced Concepts: Delving Deeper into Period and Frequency

Having explored the fundamentals of period and frequency, it’s natural to wonder how these concepts apply to more intricate scenarios. The simple inverse relationship we’ve discussed serves as a robust foundation, but the world of signals and waves is rarely composed of perfectly sinusoidal forms.

Let’s venture into some advanced topics that build upon this base, opening doors to sophisticated analytical techniques used across engineering, physics, and beyond.

Period and Frequency in Complex Waveforms

The initial examples we often encounter involve simple sine waves, characterized by a single, well-defined frequency. However, real-world signals are frequently complex waveforms, which can be thought of as the superposition of multiple sine waves with different frequencies and amplitudes.

These waveforms might appear irregular or even chaotic at first glance.

Understanding their periodic nature requires a more nuanced approach. While a complex waveform might not have a readily apparent "period" in the same way a sine wave does, it may exhibit periodicity if it repeats itself after a certain interval.

Identifying Periodicity in Complex Waveforms

The key to identifying periodicity lies in recognizing repeating patterns. This can be done visually using oscilloscopes or signal analyzers or mathematically using autocorrelation techniques.

If a complex waveform is periodic, it possesses a fundamental frequency, which is the lowest frequency component of the wave.

The period, in this case, would be the inverse of this fundamental frequency.

Harmonics and Overtones

Complex waveforms often contain harmonics or overtones, which are frequencies that are integer multiples of the fundamental frequency.

These harmonics contribute to the shape and timbre of the waveform. Analyzing the harmonic content of a signal is crucial in fields like audio engineering and vibration analysis, allowing for the identification and characterization of sound sources and mechanical systems.

Fourier Analysis and Spectral Analysis

To truly unravel the complexities of non-sinusoidal waveforms, we turn to Fourier analysis, a powerful mathematical tool that allows us to decompose a complex signal into its constituent sine waves.

At its heart, Fourier analysis rests on the principle that any periodic signal, regardless of its complexity, can be represented as a sum of sine and cosine waves with appropriate amplitudes and phases.

This decomposition process yields the frequency spectrum of the signal, which shows the amplitude of each frequency component present.

The Power of Spectral Analysis

Spectral analysis is the practical application of Fourier analysis. It allows us to visualize the frequency content of a signal, revealing hidden patterns and relationships that might not be apparent in the time domain representation.

By examining the frequency spectrum, we can identify the dominant frequencies, the presence of harmonics, and even the existence of noise or interference.

Applications of Fourier and Spectral Analysis

The applications of Fourier and spectral analysis are vast and varied.

They are fundamental to:

• Signal Processing: Filtering, compression, and noise reduction.
• Image Processing: Edge detection and image enhancement.
• Medical Diagnostics: Analyzing EEG and ECG signals.
• Telecommunications: Modulation and demodulation of signals.
• Structural Engineering: Identifying resonant frequencies in structures.

The Fast Fourier Transform (FFT)

The Fast Fourier Transform (FFT) is an efficient algorithm for computing the discrete Fourier transform (DFT), which is a numerical approximation of the Fourier transform for signals sampled at discrete points in time.

The FFT has revolutionized spectral analysis by making it computationally feasible to analyze large datasets in real time.

Tools like MATLAB, Python (with libraries like NumPy and SciPy), and specialized signal processing software provide readily available FFT implementations, empowering engineers and scientists to harness the power of Fourier analysis.

These advanced concepts build upon the foundational understanding of period and frequency, providing the tools needed to analyze and interpret complex signals in diverse fields. While they require a deeper dive into mathematical techniques, the rewards are significant, enabling a more comprehensive understanding of the world around us.

So, that’s the scoop on period from frequency! Hope this guide helps you wrap your head around it. Now go forth and conquer those frequencies!