Nyquist Explained: Unlock Digital Signal Secrets Now!

Signal processing, a critical field in modern technology, relies heavily on the foundational principles established by Harry Nyquist. The Nyquist-Shannon sampling theorem, directly related to what is nyquist, forms the backbone for converting analog signals into digital representations, a process vital for devices utilizing Digital Signal Processors (DSPs). Understanding what is nyquist is not just an academic exercise; it’s essential for anyone involved in audio engineering, telecommunications, or any field dealing with digitized information.

In today’s world, the pervasive influence of digital signals is undeniable. From the smartphones in our pockets to the sophisticated medical equipment in hospitals, digital technology underpins nearly every facet of modern life. We are surrounded by a constant stream of 0s and 1s, the language of computers, which encode and transmit information with remarkable speed and accuracy.

But how do we bridge the gap between the analog world, where information exists as continuous waves, and the digital realm, where that information is represented as discrete values? The answer lies, in part, with a set of principles pioneered by Harry Nyquist.

What is Nyquist? Unveiling the Digital Enigma

At the heart of understanding digital signal processing lies a fundamental question: What is Nyquist?

This seemingly simple question unlocks a universe of concepts related to sampling, signal reconstruction, and the very limits of digital representation.

The name "Nyquist" is attached to several crucial concepts in the field, including the Nyquist Rate and the Nyquist Frequency. These terms are not mere technical jargon; they are the cornerstones upon which the digital revolution has been built.

Our Objective: Demystifying Key Principles

This article aims to demystify the core principles associated with Nyquist, specifically the Nyquist Rate, the Nyquist Frequency, and the underlying theorem that governs them.

We will explore the essential relationship between these concepts and their practical implications for various technologies.

By the end of this exploration, you will gain a solid understanding of how these principles work and why they are essential for ensuring the integrity and accuracy of digital signals in countless applications.

The Fundamentals: Analog to Digital Conversion and Sampling

Before diving into the specifics of the Nyquist Rate and Frequency, it’s crucial to understand the foundational process of converting analog signals into their digital counterparts. After all, the Nyquist theorem directly addresses the constraints and possibilities inherent in this conversion. Let’s examine how we transform the continuous world of analog into the discrete language of digital.

Bridging the Gap: Analog to Digital Conversion

The world around us is inherently analog. Sound waves, light, temperature – these phenomena exist as continuous variations in magnitude.

However, computers operate using digital signals, which are discrete representations of information using binary digits (bits).

To process real-world information, we need to translate these analog signals into a digital format that computers can understand. This translation happens through a process called analog-to-digital conversion (ADC).

The Sampling Process: Capturing Snapshots in Time

At the heart of ADC lies the concept of sampling.

Sampling involves measuring the amplitude of an analog signal at regular intervals. Think of it like taking snapshots of a moving object at fixed points in time.

Each snapshot captures the instantaneous value of the analog signal at that specific moment. These snapshots are called samples.

The ADC then converts each sample into a digital value, represented by a finite number of bits. This process essentially quantizes the continuous analog signal into a series of discrete digital values.

Sampling Rate: Dictating the Granularity

The sampling rate is a critical parameter in the ADC process. It defines how many samples are taken per unit of time, typically measured in Hertz (Hz) or samples per second.

A higher sampling rate means that more samples are taken per second, resulting in a more detailed representation of the original analog signal.

Imagine filming a scene with a high frame rate versus a low frame rate – the higher frame rate will capture more subtle movements and details. Similarly, a higher sampling rate captures more nuances of the analog signal.

The Link Between Sampling Rate and Signal Quality

The sampling rate directly impacts the quality and precision of the resulting digital signal.

A higher sampling rate generally leads to a more accurate representation of the original analog signal. This is because more samples capture more of the signal’s information.

Conversely, a lower sampling rate may miss important details and lead to a less accurate representation. In extreme cases, a sampling rate that is too low can result in a phenomenon known as aliasing, which we will address later.

Therefore, choosing an appropriate sampling rate is crucial for ensuring the fidelity of the digital signal. This choice is governed by the principles of the Nyquist-Shannon Sampling Theorem, which provides a theoretical lower bound on the sampling rate required to accurately reconstruct an analog signal from its digital samples.

Harry Nyquist: The Man Behind the Theorem

Before we delve deeper into the intricacies of the Nyquist-Shannon Sampling Theorem, it’s essential to acknowledge the brilliant mind behind it: Harry Nyquist. His work laid the very foundation for our understanding of digital signal processing and information theory. Understanding his background and the context of his research provides valuable insight into the significance of his contributions.

A Pioneer in Information Theory

Harry Nyquist (1889-1976) was a Swedish-born American physicist and engineer. He made groundbreaking contributions to both information theory and signal processing during his long and distinguished career at Bell Telephone Laboratories.

His work during the early 20th century helped pave the way for the digital age.

Nyquist’s early research focused on thermal noise in electrical conductors. He also studied the stability of feedback amplifiers – research that led to the development of the Nyquist stability criterion.

This criterion remains a fundamental tool in control systems engineering even today.

The Bell Labs Environment: A Crucible of Innovation

Nyquist’s contributions were deeply rooted in the innovative environment of Bell Labs. During his time there, Bell Labs was a hotbed of scientific and technological breakthroughs.

Researchers were actively pushing the boundaries of communication technology. They explored new ways to transmit information more efficiently and reliably.

This fertile intellectual landscape fostered collaboration and cross-disciplinary thinking, allowing Nyquist to draw upon diverse areas of expertise. This is where his insights on signal transmission and sampling started to take form.

Establishing Fundamental Limits: The Nyquist Rate

One of Nyquist’s most profound achievements was identifying the fundamental limits of data transmission over a channel with limited bandwidth.

His work, along with that of Claude Shannon, established the theoretical basis for understanding how much information could be reliably transmitted through a communication channel.

The Nyquist Rate, derived from his work, dictates the minimum sampling rate required to accurately capture an analog signal.

This concept is at the heart of analog-to-digital conversion and digital signal processing. It ensures faithful representation and reconstruction of the original signal.

Nyquist’s legacy extends far beyond the specific theorem that bears his name. His work touched on numerous aspects of communications engineering. It forever altered how we approach signal processing and data transmission.

Nyquist’s work at Bell Labs established crucial foundations for understanding signal behavior.

This groundwork now allows us to fully grasp the implications of the Nyquist-Shannon Sampling Theorem, the cornerstone of digital signal processing. This theorem dictates the conditions necessary for perfectly capturing and reconstructing analog signals in the digital domain.

The Nyquist-Shannon Sampling Theorem: The Core Principle Explained

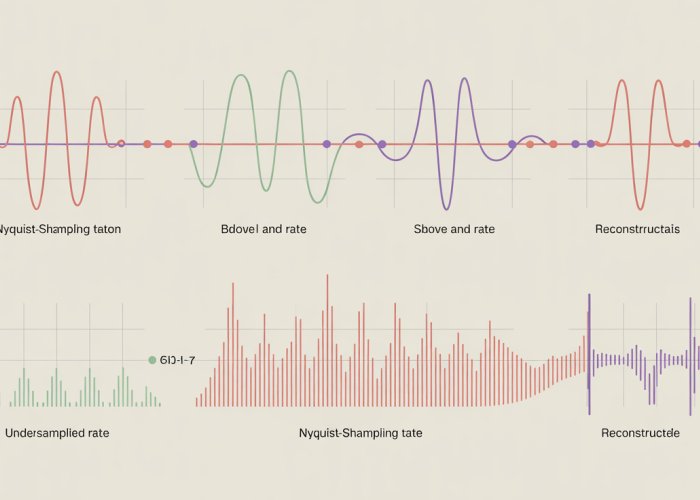
The Nyquist-Shannon Sampling Theorem, often simply called the Sampling Theorem, is a fundamental principle in the field of signal processing. It elegantly defines the minimum rate at which an analog signal must be sampled to accurately reconstruct it from its digital samples. This rate is inextricably linked to the highest frequency component present in the original signal.

At its core, the theorem states: To perfectly reconstruct an analog signal from its digital samples, the sampling rate must be at least twice the highest frequency component of the original signal.

This "twice the highest frequency" benchmark is crucial.

Defining the Nyquist Rate: The Key to Accurate Reconstruction

The Nyquist Rate represents the minimum sampling rate required to avoid losing information during the analog-to-digital conversion. Sampling at or above the Nyquist Rate guarantees that all the information present in the original signal is captured, allowing for perfect reconstruction.

In simpler terms, if you want to create a faithful digital copy of an analog signal, you must sample it frequently enough.

The Nyquist Rate mathematically equals to twice the highest frequency present in the signal.

Failing to meet this rate leads to a phenomenon known as aliasing, which we will explore later.

Unveiling the Nyquist Frequency: The Upper Limit

The Nyquist Frequency, in contrast to the Nyquist Rate, describes a frequency boundary.

It is defined as half of the sampling rate.

Think of it as the highest frequency that a digitally sampled system can accurately represent. Any frequency component in the original analog signal above the Nyquist Frequency will be misinterpreted during the sampling process, leading to distortion and inaccuracies in the reconstructed signal.

The Interplay: Sampling Rate, Nyquist Rate, and Nyquist Frequency

It’s crucial to understand the relationship between these three interconnected concepts:

• Sampling Rate: The frequency at which the analog signal is sampled (samples per second).
• Nyquist Rate: The minimum required sampling rate, which is twice the highest frequency in the signal.
• Nyquist Frequency: Half of the sampling rate, representing the highest frequency accurately capturable.

If the Sampling Rate is greater than or equal to the Nyquist Rate, accurate reconstruction is possible. If the Sampling Rate is less than the Nyquist Rate, aliasing will occur. The Nyquist Frequency serves as a critical threshold; frequency components above this value pose a problem.

In essence, the Sampling Rate sets the stage. The Nyquist Rate defines the bare minimum, and the Nyquist Frequency marks the upper limit for faithful digital representation. When these elements are in harmony, the digital world accurately mirrors its analog counterpart.

Aliasing: The Undesirable Artifact of Undersampling

The Nyquist-Shannon Sampling Theorem provides the rules for successful analog-to-digital conversion. But what happens when we break the rules?

Failing to adhere to the Nyquist Rate opens the door to a particularly troublesome phenomenon: aliasing. It’s a distortion that fundamentally alters the frequency components of a signal, leading to inaccurate representations and potentially disastrous consequences in signal processing.

Understanding the Root Cause of Aliasing

At its core, aliasing arises when the sampling rate falls below the Nyquist Rate. In these conditions, high-frequency components in the analog signal are not captured adequately during the sampling process. Instead, they are misinterpreted as lower frequencies.

This misinterpretation happens because the sampling process effectively creates "aliases" of the higher frequencies at lower frequency ranges.

Imagine trying to photograph a rapidly spinning fan with a slow camera shutter. Instead of seeing a blur or a complete rotation, you might capture distinct, but incorrect, positions of the fan blades. The fan appears to be rotating much slower, or even in the opposite direction. This is a visual analogy of what aliasing does to signals.

Frequencies Above the Nyquist Frequency: A Case of Mistaken Identity

The Nyquist Frequency, defined as half the sampling rate, acts as a critical boundary. Any frequency component above this limit is vulnerable to aliasing. When such a high-frequency component is sampled below the Nyquist Rate, the resulting samples are indistinguishable from those of a lower-frequency signal.

The system essentially "folds" the high-frequency component back into the lower frequency range, creating a false representation. This means the digitized signal will contain frequencies that weren’t actually present in the original analog signal.

The "Wagon Wheel Effect" and Other Visual Manifestations

One of the most common and easily understood examples of aliasing is the "wagon wheel effect" often seen in movies. As a wagon wheel spins faster, there’s a point where it appears to slow down, stop, and then rotate backward.

This isn’t because the wheel is actually changing direction. Instead, the camera’s frame rate (its sampling rate for capturing motion) is too low to accurately capture the wheel’s rapid rotation. Each frame captures the wheel in a slightly different position. Due to undersampling, the brain interprets these positions as a slower, or even reversed, rotation.

This effect demonstrates how aliasing can create completely false perceptions of movement and frequency.

Beyond the wagon wheel, aliasing can manifest in various other ways, including:

• Audio Distortion: In audio recordings, aliasing can introduce unwanted tones and harsh artifacts, degrading the overall sound quality.
• Image Artifacts: In images, it can lead to jagged edges, moiré patterns, and other visual distortions that obscure the details of the scene.
• Data Misinterpretation: In scientific and engineering applications, aliasing can lead to incorrect measurements and flawed conclusions, impacting the accuracy and reliability of the data.

Understanding the mechanisms and visual signs of aliasing is crucial for recognizing and mitigating its impact on digital signal processing.

Frequencies Above the Nyquist Frequency: A Case of Mistaken Identity

The Nyquist Frequency, defined as half the sampling rate, acts as a critical boundary. Any frequency component above this limit is vulnerable to aliasing. When such a high-frequency component is sampled below the Nyquist Rate, the resulting samples are indistinguishable from those of a lower-frequency signal.

The system essentially "folds" the high-frequency component back into the lower-frequency range, creating a false representation. But if we know this to be true, what is the solution?

Anti-Aliasing Filters: Guarding Against Signal Distortion

The solution to the aliasing problem lies in preventing those problematic high-frequency components from ever reaching the sampler in the first place. This is where anti-aliasing filters come into play.

The Role of Anti-Aliasing Filters

An anti-aliasing filter is a crucial component in any system that converts analog signals to digital signals. Its primary purpose is to remove or significantly attenuate frequencies above the Nyquist Frequency before the sampling process occurs.

By doing so, it ensures that the sampling process only deals with frequencies that can be accurately represented, preventing the generation of spurious alias frequencies.

Think of it as a gatekeeper, carefully screening the incoming signal and blocking any frequencies that could cause trouble.

How Anti-Aliasing Filters Work

These filters are typically low-pass filters, designed to allow frequencies below a certain cutoff frequency to pass through while attenuating frequencies above that cutoff. The cutoff frequency is usually set close to, but below, the Nyquist Frequency.

The design and characteristics of the filter are critical. A sharp cutoff is desirable to effectively eliminate unwanted frequencies. However, extremely sharp cutoffs can introduce other undesirable effects like phase distortion, requiring a trade-off in filter design.

The goal is to achieve a balance between effective alias suppression and minimal signal alteration within the desired frequency range.

Practical Considerations in Filter Selection

Choosing the right anti-aliasing filter involves considering several practical factors:

• Cutoff Frequency: The cutoff frequency must be carefully selected based on the sampling rate and the characteristics of the input signal.

• Filter Order: A higher-order filter provides a steeper roll-off, more effectively attenuating frequencies above the cutoff. However, higher-order filters also tend to be more complex and can introduce more phase distortion.

• Filter Type: Various filter types (e.g., Butterworth, Chebyshev, Bessel) offer different trade-offs between cutoff sharpness, passband flatness, and phase response.

• Phase Response: Linear phase response is often desirable to minimize signal distortion.

• Cost and Complexity: The cost and complexity of the filter must be weighed against the desired performance.

Ultimately, the selection of an anti-aliasing filter is a balancing act, requiring careful consideration of the specific application requirements and the trade-offs between various filter characteristics. Without these considerations, aliasing will occur and could have significant and unintended consequences.

The effectiveness of anti-aliasing filters in safeguarding signal integrity might seem theoretical, but the ramifications of the Nyquist theorem and the tools that stem from it are deeply embedded in the technology that shapes our daily experiences. Let’s examine where and how this principle is essential.

Real-World Applications: Nyquist in Action Across Industries

The Nyquist-Shannon Sampling Theorem isn’t just an abstract mathematical concept; it’s a cornerstone of modern technology, quietly but powerfully shaping how we interact with the digital world. From capturing sound to transmitting data, the theorem’s principles are at play, ensuring the fidelity and accuracy of digital representations of analog signals.

Data Acquisition: Capturing the Analog World

Data acquisition systems are the bridge between the analog and digital realms, collecting real-world signals such as temperature, pressure, and voltage. These systems rely heavily on the Nyquist theorem to ensure that the acquired data accurately reflects the original analog signal.

Undersampling in data acquisition can lead to disastrous consequences, misrepresenting critical data and potentially leading to incorrect analyses or control decisions.

ADC (Analog-to-Digital Converter): The Sampling Heart

At the heart of every data acquisition system lies the Analog-to-Digital Converter (ADC). The ADC’s sampling rate must be carefully chosen, adhering to the Nyquist Rate, to avoid aliasing and ensure accurate conversion. Sophisticated ADCs often incorporate anti-aliasing filters to further protect against signal distortion.

DAC (Digital-to-Analog Converter): Reconstructing the Signal

Conversely, Digital-to-Analog Converters (DACs) reconstruct analog signals from digital data.

While the Nyquist theorem primarily concerns the sampling process (analog-to-digital conversion), its principles extend to the reconstruction process as well. The quality of the reconstructed signal is directly related to the original sampling rate and the DAC’s ability to accurately reproduce the sampled data.

Audio Engineering: The Sound of Fidelity

In audio engineering, the Nyquist theorem is paramount. Digital audio relies entirely on the accurate conversion of sound waves into digital samples, and any deviation from the Nyquist Rate can result in audible artifacts and a loss of fidelity.

The standard sampling rate for CDs, 44.1 kHz, was chosen based on the Nyquist theorem, ensuring that frequencies up to approximately 20 kHz (the upper limit of human hearing) can be accurately captured.

Professional audio workstations and high-resolution audio formats often utilize even higher sampling rates to provide additional headroom and minimize potential aliasing effects, particularly when complex audio processing is involved.

Image Processing: Capturing Visual Reality

Image processing, from digital photography to medical imaging, also relies on the principles of the Nyquist theorem. When an image is captured by a digital sensor, the light intensity at discrete points is sampled.

If the sampling rate (the density of pixels on the sensor) is too low, aliasing can occur, resulting in unwanted artifacts such as moiré patterns or jagged edges.

The Moire Effect

The moiré effect, a common example of aliasing in image processing, appears as wavy patterns when capturing images with repetitive structures (e.g., fabrics or fine lines).

Anti-aliasing techniques, such as blurring the image slightly before sampling or using specialized sensor designs, are employed to mitigate these effects and improve image quality.

Telecommunications: Transmitting Information Reliably

The Nyquist theorem is also crucial in telecommunications, where signals are transmitted over various channels.

To ensure reliable communication, the sampling rate used to digitize the signal must be high enough to capture all the relevant frequency components.

Modern Communication

Modern communication systems employ sophisticated modulation and coding techniques, but the underlying principle of the Nyquist theorem remains essential for accurately representing and transmitting information. From voice calls to streaming video, the theorem plays a critical role in ensuring clear and reliable communication.

Implications, Limitations, and Practical Challenges

While the Nyquist theorem provides a crucial theoretical foundation, its influence extends far beyond textbook equations. Understanding its implications, limitations, and the practical hurdles it presents is vital for anyone working with digital systems.

Broad Implications Across Diverse Fields

The Nyquist-Shannon Sampling Theorem has profound implications across numerous fields. It’s not just about audio recording or image processing; its principles are integral to:

• Telecommunications: Ensuring reliable data transmission by setting minimum sampling rates for digital communication channels.

• Medical Imaging: From MRI to CT scans, the theorem dictates the necessary sampling resolution to capture accurate anatomical details.

• Scientific Instrumentation: Any instrument that digitizes analog signals, such as oscilloscopes and spectrum analyzers, relies on Nyquist to faithfully record data.

• Control Systems: In feedback control, accurately representing sensor data is critical for stable and responsive systems.

In each of these areas, the correct application of the Nyquist theorem is critical for data integrity.

Limitations and Real-World Obstacles

Despite its power, the Nyquist Theorem isn’t a silver bullet. It operates under idealized conditions, and real-world scenarios often present challenges.

One key limitation is the assumption of bandlimited signals—signals with a defined maximum frequency. In reality, many signals contain high-frequency components that are difficult or impossible to eliminate entirely.

The Ideal Filter Fallacy

Anti-aliasing filters, while crucial, are not perfect "brick walls." Real filters have a transition band, where frequencies are attenuated but not entirely eliminated.

This means some aliasing is almost always present, requiring a careful trade-off between filter complexity and signal fidelity.

Noise Considerations

The Nyquist theorem doesn’t account for noise. In noisy environments, a higher sampling rate than theoretically required may be necessary to improve the signal-to-noise ratio and facilitate accurate signal reconstruction.

Computational Cost

Higher sampling rates increase the volume of data that must be processed and stored. This can impose significant computational burdens, especially in real-time applications with limited resources.

Practical Challenges in Digital System Design

Designing robust digital systems requires careful consideration of the Nyquist Rate alongside other engineering constraints.

Selecting the appropriate sampling rate involves balancing the need for accuracy with the limitations of hardware, processing power, and storage capacity.

Jitter and Clock Stability

The Nyquist theorem assumes a perfectly stable sampling clock. In practice, timing jitter can introduce errors that effectively reduce the usable bandwidth.

Signal Conditioning

Proper signal conditioning is essential to ensure that the input signal is within the ADC’s dynamic range and free from excessive noise.

System-Level Design

Meeting the Nyquist criterion is just one piece of the puzzle. A successful digital system requires careful integration of all components, from sensors to processing algorithms to output devices.

Ultimately, a thorough understanding of the Nyquist theorem, its limitations, and the practical challenges involved is essential for designing high-performance and reliable digital systems. It allows engineers to make informed decisions and trade-offs.

So, you’ve now got a handle on what is nyquist! Hopefully, this clears things up and gives you a solid foundation to explore digital signals further. Go forth and conquer those signals!