Net Force Formula: Master it Now! Physics Made Simple

Isaac Newton’s groundbreaking work on classical mechanics provides the foundation for understanding force. This foundation enables the accurate calculation of acceleration, a crucial attribute in physics; subsequently, the net force formula emerges as a central concept for solving problems related to motion. Numerous online physics simulations demonstrate the application of this formula, revealing how forces interact to produce a resultant force. Mastering the net force formula unlocks comprehension of dynamic systems studied across various engineering disciplines, from NASA’s aerospace projects to civil engineering constructions. Therefore, grasping the net force formula is essential for anyone seeking proficiency in physics and related fields.

From the gentle push of a door to the immense power of a rocket launch, force governs the world around us. Though often unseen, forces are the invisible hands that dictate how objects move, accelerate, or remain at rest. Understanding these interactions is fundamental to grasping the principles of physics.

At the heart of this understanding lies the concept of net force. It’s not enough to simply acknowledge individual forces; we must consider their combined effect. The net force is the vector sum of all forces acting on an object. It’s the ultimate determinant of its motion.

The Ubiquitous Nature of Force

Force is not an abstract concept confined to textbooks. It’s an integral part of our daily experiences. Consider these examples:

• Walking: Each step involves friction between your shoes and the ground, propelling you forward.
• Lifting an object: You exert an upward force to counteract gravity’s downward pull.
• Driving a car: The engine provides a forward force, while friction and air resistance oppose its motion.
• A ball thrown in the air: Once released from your hand, gravity acts upon the ball, pulling it back down toward the Earth

These are just a few examples of how forces are constantly at play, shaping our interactions with the physical world.

Why Net Force Matters

Understanding net force is paramount in physics because it directly determines an object’s acceleration, or change in velocity. It bridges the gap between forces and motion, allowing us to predict and explain how objects will behave under different conditions.

• Predicting Motion: By knowing the net force acting on an object, we can calculate its acceleration and, consequently, predict its future position and velocity.
• Understanding Equilibrium: When the net force on an object is zero, the object is in equilibrium, meaning it remains at rest or continues to move at a constant velocity. This principle is crucial in engineering and construction.
• Analyzing Complex Systems: Many real-world scenarios involve multiple forces acting simultaneously. Understanding net force enables us to break down these complex systems into manageable components and analyze their overall behavior.

Demystifying the Net Force Formula

The goal of this discussion is to demystify the net force formula and make it accessible to everyone. We aim to break down the formula into its fundamental components, explain each variable in detail, and illustrate its application through practical examples.

By the end of this exploration, you’ll have a solid grasp of the net force formula and its significance in understanding the physical world. It will provide a foundational knowledge for more advanced physics concepts.

From the gentle push of a door to the immense power of a rocket launch, force governs the world around us. Though often unseen, forces are the invisible hands that dictate how objects move, accelerate, or remain at rest. Understanding these interactions is fundamental to grasping the principles of physics.

At the heart of this understanding lies the concept of net force. It’s not enough to simply acknowledge individual forces; we must consider their combined effect. The net force is the vector sum of all forces acting on an object. It’s the ultimate determinant of its motion.

The Ubiquitous Nature of Force
Force is not an abstract concept confined to textbooks. It’s an integral part of our daily experiences. Consider these examples:

Walking: Each step involves friction between your shoes and the ground, propelling you forward.

Lifting an object: You exert an upward force to counteract gravity’s downward pull.

Driving a car: The engine provides a forward force, while friction and air resistance oppose its motion.

A ball thrown in the air: Once released from your hand, gravity acts upon the ball, pulling it back down toward the Earth

These are just a few examples of how forces are constantly at play, shaping our interactions with the physical world.

Why Net Force Matters
Understanding net force is paramount in physics because it directly determines an object’s acceleration, or change in velocity. It bridges the gap between forces and motion, allowing us to predict and explain how objects will behave under… Understanding the why behind the net force requires us to first establish a solid foundation in the core concepts that underpin it: force itself, mass, and acceleration. Without a firm grasp of these fundamentals, the net force formula remains merely a collection of symbols rather than a powerful tool for understanding the physical world.

Fundamentals of Force, Mass, and Acceleration

Before diving into the intricacies of net force, it’s crucial to solidify our understanding of three fundamental concepts: force, mass, and acceleration. These are the building blocks upon which the entire framework of Newtonian mechanics rests.

Defining Force

At its core, force is an interaction that, when unopposed, will change the motion of an object. This change can manifest as acceleration, a change in velocity, or a deformation of the object.

Think of pushing a box across the floor, or the Earth pulling an apple from a tree. These are all examples of force in action.

Force is a vector quantity, meaning it has both magnitude and direction. The standard unit of force is the Newton (N), which we will explore in more detail later when we discuss the net force formula.

Understanding Mass

Mass is a fundamental property of matter that measures its resistance to acceleration. In other words, it’s a measure of an object’s inertia.

The more massive an object is, the harder it is to change its state of motion. Imagine trying to push a shopping cart versus pushing a loaded truck; the truck is much more difficult to accelerate because it has significantly more mass.

The standard unit of mass is the kilogram (kg). It is important to differentiate mass from weight, which is the force of gravity acting on an object’s mass.

Mass as Inertia

Inertia, closely associated with mass, is an object’s inherent resistance to changes in its velocity. This resistance means an object will stay at rest if it’s at rest, or it will continue moving at a constant velocity if it’s in motion, unless acted upon by an external force.

Deciphering Acceleration

Acceleration is the rate at which an object’s velocity changes over time. This change can be in speed, direction, or both. A car speeding up, a ball changing direction, or even a satellite orbiting Earth—all involve acceleration.

Acceleration is also a vector quantity, possessing both magnitude and direction. Its standard unit is meters per second squared (m/s²).

The Link Between Force and Acceleration

Forces are responsible for causing acceleration. When a net force acts on an object, it accelerates in the direction of the force. The greater the force, the greater the acceleration, assuming the mass remains constant. This direct relationship between force and acceleration is a cornerstone of classical mechanics, and we will explore it further in the context of Newton’s Second Law.

Understanding net force is paramount in physics because it directly determines an object’s acceleration, or change in velocity. It bridges the gap between forces and motion, allowing us to predict and explain how objects will behave under different conditions. Now, we’ll delve into the core of this relationship by exploring the net force formula itself.

The Net Force Formula: Fnet = ma

At the heart of understanding how forces dictate motion lies a simple yet powerful equation: Fnet = ma. This formula is the cornerstone of classical mechanics and provides a quantitative link between force, mass, and acceleration. Let’s break it down to understand the meaning and implications of each component.

Defining Net Force

Net force is not simply any single force acting on an object. Instead, it is the vector sum of all forces. This means we must consider both the magnitude and direction of each force when determining the overall effect.

If multiple forces act in the same direction, their magnitudes add together. If they act in opposite directions, their magnitudes subtract. The resulting net force represents the single, effective force that influences the object’s motion. Without understanding that it’s the resultant of all forces combined, it’s just looking at one piece of the puzzle.

Dissecting the Formula: Fnet = ma

The equation Fnet = ma concisely captures the relationship between net force, mass, and acceleration. Each variable plays a critical role:

• Fnet: Represents the net force acting on the object. It’s crucial to remember that this is the vector sum of all forces involved, not just one isolated force.
• m: Stands for the mass of the object. Mass is a measure of an object’s inertia, or its resistance to acceleration. The greater the mass, the more force is required to produce a given acceleration.
• a: Denotes the acceleration of the object. Acceleration is the rate at which an object’s velocity changes over time. It is directly proportional to the net force and inversely proportional to the mass.

Net Force (Fnet): Meaning and Units

Net force (Fnet) as we discussed, is the overall force acting on an object after considering all individual forces and their directions. It’s measured in Newtons (N).

Mass (m): The Role of Inertia

Mass (m) is a fundamental property of matter that quantifies its resistance to acceleration. The greater the mass, the more force is required to achieve the same acceleration.

Mass is typically measured in kilograms (kg).

Acceleration (a): Linking Force and Motion

Acceleration (a) describes how quickly an object’s velocity changes over time. It’s the direct result of a net force acting on a mass.

Acceleration is measured in meters per second squared (m/s²).

Units of Measurement: The Importance of Newtons

In the Fnet = ma formula, it’s critical to use consistent units of measurement. The standard unit of force is the Newton (N).

One Newton is defined as the force required to accelerate a 1-kilogram mass at a rate of 1 meter per second squared (1 N = 1 kg m/s²*). This dimensional consistency ensures that our calculations are accurate and meaningful.

Understanding the units and their relationships is essential for applying the net force formula correctly. Always double-check that your units are consistent before performing any calculations.

Dissecting the Formula: Fnet = ma

The equation Fnet = ma concisely captures the relationship between net force, mass, and acceleration. Each variable plays a critical role:

Fnet: Represents the net force acting on the object. It’s crucial to remember that this is…

Newton’s Second Law: The Foundation of Net Force

Having established the net force formula, it’s crucial to understand where it originates and why it holds such significance. The answer lies in Newton’s Second Law of Motion, a fundamental principle governing the behavior of objects in motion. This law isn’t just a mathematical equation; it’s a statement about the very nature of force and its impact on the world around us.

Unveiling Newton’s Laws of Motion

Newton formulated three laws of motion that form the bedrock of classical mechanics. While all three laws are essential, the Second Law is the one that directly incorporates the concept of net force.

The First Law, the Law of Inertia, states that an object at rest stays at rest, and an object in motion stays in motion with the same speed and in the same direction unless acted upon by a net force. The Third Law states that for every action, there is an equal and opposite reaction.

It is the Second Law that gives us the quantitative relationship between force and motion.

The Second Law: Net Force and Acceleration

Newton’s Second Law of Motion formally states that the acceleration of an object is directly proportional to the net force acting on it, is in the same direction as the net force, and is inversely proportional to the mass of the object. This is precisely what the formula Fnet = ma expresses.

In simpler terms, if you apply a net force to an object, it will accelerate in the direction of that force. The greater the force, the greater the acceleration.

Conversely, the more massive the object, the less it will accelerate for the same amount of force.

Net Force Dictates Acceleration

The power of Newton’s Second Law lies in its ability to predict and explain motion. If we know the net force acting on an object and its mass, we can determine its acceleration. This allows us to understand how an object’s velocity will change over time.

Imagine pushing a box across a smooth floor. The harder you push (the greater the net force), the faster the box accelerates. If the box is filled with heavy items (increasing its mass), it will accelerate more slowly for the same push.

This intuitive relationship is exactly what Newton’s Second Law describes mathematically. Without a net force, there is no acceleration, and the object maintains its current state of motion (or rest). This underlines the importance of identifying and calculating net force when analyzing physical systems.

Proportional Relationship Explained

The Second Law highlights a direct proportional relationship between net force and acceleration. Direct proportionality means that if you double the net force, you double the acceleration, assuming the mass remains constant. Similarly, if you triple the net force, you triple the acceleration, and so on.

This relationship underscores the central role of net force in determining an object’s motion. It’s not just about any force, but the net or resultant force that truly dictates how an object responds. Understanding this proportional relationship is vital for predicting and controlling motion in a variety of applications, from designing vehicles to analyzing projectile trajectories.

Having established the fundamental link between net force and acceleration through Newton’s Second Law, it’s time to ground these abstract concepts in the tangible world. Forces are not just theoretical constructs; they are the invisible hands that shape our daily experiences. Understanding the common types of forces at play allows us to analyze and predict motion in a more intuitive way.

Exploring Common Forces in Action

The world around us is a constant interplay of various forces, each with its unique characteristics and effects. From the moment we wake up to the time we go to sleep, these forces are subtly and not-so-subtly influencing our actions and the behavior of objects. Let’s delve into some of the most prevalent forces, examining their nature and significance.

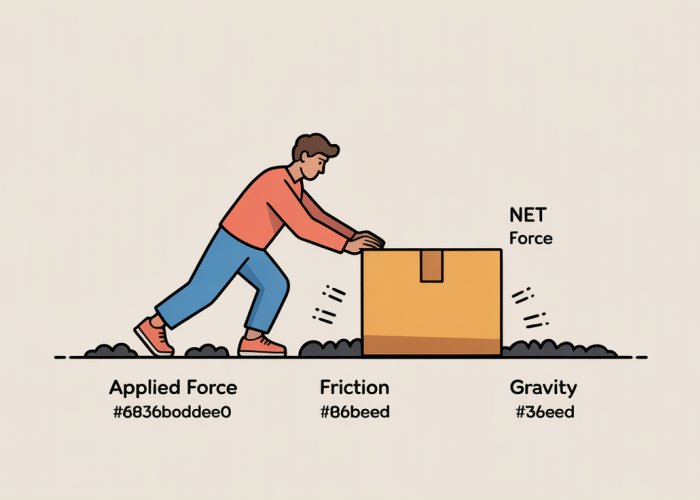
Gravity: The Universal Attraction

Gravity is perhaps the most ubiquitous force we experience. It’s the force of attraction between any two objects with mass. On Earth, we primarily experience the gravitational pull of our planet, keeping us grounded and dictating the trajectory of objects thrown into the air.

The strength of gravity depends on the masses of the objects and the distance between them. This is why we are so strongly affected by the Earth’s gravity – the Earth has an immense mass.

Weight: The Force of Gravity on Mass

Weight is often used interchangeably with mass, but they are fundamentally different concepts. Weight is the force of gravity acting on an object’s mass. Therefore, weight is a force, measured in Newtons (N), while mass is a measure of inertia, measured in kilograms (kg).

Weight can be calculated using the formula: W = mg, where ‘W’ is weight, ‘m’ is mass, and ‘g’ is the acceleration due to gravity (approximately 9.8 m/s² on Earth).

It is also very important to keep in mind that your weight can change if you were to travel to another planet (different gravitational pull) , but your mass will remain the same.

Normal Force: Resisting Compression

The normal force is a contact force exerted by a surface on an object in response to the object’s weight or any other force pressing it against the surface. It acts perpendicular to the surface, preventing the object from passing through it.

For example, when you stand on the floor, the floor exerts an upward normal force on you, counteracting the downward force of your weight. The magnitude of the normal force often equals the weight of the object, but it can vary depending on other forces acting on the object and the angle of the surface.

Applied Force: The Direct Push or Pull

An applied force is any force that we directly exert on an object. This could be a push, a pull, or any other direct contact force. Examples include pushing a box across the floor, pulling a wagon, or lifting a book.

The magnitude and direction of the applied force determine its effect on the object’s motion. It’s a tangible force, readily observable and controlled.

Friction: The Resistance to Motion

Friction is a force that opposes motion between surfaces in contact. It arises from the microscopic irregularities and interactions between the surfaces.

Friction can be static (preventing motion from starting) or kinetic (opposing motion that is already occurring). It plays a crucial role in many everyday phenomena, from allowing us to walk without slipping to providing the necessary grip for car tires to move. The rougher the surfaces, the greater the frictional force. Friction always acts in the opposite direction of motion (or intended motion).

Having established the fundamental link between net force and acceleration through Newton’s Second Law, it’s time to ground these abstract concepts in the tangible world. Forces are not just theoretical constructs; they are the invisible hands that shape our daily experiences. Understanding the common types of forces at play allows us to analyze and predict motion in a more intuitive way.

Visualizing Forces: The Power of Free Body Diagrams

To truly master the concept of net force, we need a powerful tool for visualizing and analyzing the forces acting on an object: the Free Body Diagram (FBD). Think of FBDs as a blueprint for understanding motion; they strip away the complexities of a real-world scenario and focus solely on the forces at play.

What is a Free Body Diagram?

A Free Body Diagram is a simplified representation of an object, showing all the forces acting on it. The object itself is typically represented as a simple box or dot, and the forces are drawn as arrows pointing away from the object, indicating their direction and relative magnitude.

Essentially, FBDs isolate the object of interest and its interactions with the surrounding environment in terms of forces. This allows us to systematically analyze each force and determine its contribution to the net force.

Creating a Free Body Diagram: A Step-by-Step Guide

Creating a Free Body Diagram is a straightforward process:

1. Identify the Object: Determine which object you are analyzing. This is the "free body."

2. Represent the Object: Draw a simple shape (box, dot, or circle) to represent the object. The shape isn’t important; it’s just a placeholder.

3. Identify All Forces: List all the forces acting on the object. Consider forces like gravity, applied force, friction, normal force, tension, etc.

   • Don’t include forces the object exerts on other objects. Only include forces exerted on the object you are analyzing.

4. Draw Force Vectors: Draw arrows representing each force, starting from the center of the object and pointing in the direction the force is acting.

   • The length of the arrow should be proportional to the magnitude of the force (longer arrow = larger force).
   • Label each force vector clearly (e.g., Fg for gravity, Fn for normal force, Fa for applied force, Ff for friction).

5. Establish a Coordinate System: Choose a coordinate system (x and y axes) to help resolve forces into components. This is especially important for inclined plane problems.

How Free Body Diagrams Aid in Calculating Net Force

Free Body Diagrams are invaluable because they provide a clear visual representation of all the forces contributing to the net force. By visually representing the forces, it becomes much easier to:

• Identify all forces: Ensure no forces are missed in the analysis.
• Determine directions: Clearly see the direction of each force, which is crucial for vector addition.
• Resolve forces into components: Break down forces into their x and y components using trigonometry, if necessary.
• Apply Newton’s Second Law: Use the FBD to apply Fnet = ma, calculating the net force and subsequently the acceleration of the object.

The FBD acts as a bridge, connecting the qualitative understanding of forces to the quantitative calculation of net force and motion.

Examples of Free Body Diagrams

Let’s look at some common scenarios and their corresponding Free Body Diagrams:

Object at Rest on a Horizontal Surface

• Forces: Gravity (Fg) acting downward, Normal Force (Fn) acting upward.
• Analysis: The Normal Force balances the force of Gravity, resulting in zero net force and no acceleration (static equilibrium).

Object Being Pushed Horizontally Across a Surface

• Forces: Gravity (Fg) acting downward, Normal Force (Fn) acting upward, Applied Force (Fa) acting horizontally, Friction (Ff) acting horizontally in the opposite direction of motion.
• Analysis: The net force in the horizontal direction is Fa – Ff. If Fa > Ff, the object accelerates in the direction of the applied force.

Object on an Inclined Plane

• Forces: Gravity (Fg) acting downward, Normal Force (Fn) acting perpendicular to the plane, Friction (Ff) acting parallel to the plane and opposing motion.
• Analysis: Gravity is resolved into components parallel and perpendicular to the plane. The component parallel to the plane causes the object to slide down, while friction opposes this motion.

In each of these examples, the Free Body Diagram allows us to visualize the forces, understand their relationships, and ultimately calculate the net force acting on the object. By mastering the art of creating and interpreting FBDs, you gain a powerful tool for understanding and predicting motion in a wide range of physical scenarios.

Having established the fundamental link between net force and acceleration through Newton’s Second Law, it’s time to ground these abstract concepts in the tangible world. Forces are not just theoretical constructs; they are the invisible hands that shape our daily experiences. Understanding the common types of forces at play allows us to analyze and predict motion in a more intuitive way. Visualizing these forces with tools like Free Body Diagrams further empowers us to understand their effect on an object. Now, let’s translate these diagrams and laws into concrete numerical solutions.

Calculating Net Force: From Theory to Practice

The real power of the net force equation, Fnet = ma, lies in its ability to quantify and predict motion. Let’s move beyond the theoretical and delve into practical applications.

This section will walk through a series of worked examples, demonstrating how to calculate the net force in diverse scenarios.

We’ll start with simple horizontal forces, then tackle the complexities of inclined planes, and finally address situations with multiple forces acting at various angles. Each example will break down the process step-by-step, highlighting key concepts and techniques.

Simple Horizontal Force Problems: A Straightforward Approach

Let’s begin with the simplest case: an object moving horizontally with a constant acceleration.

Consider a box with a mass of 5 kg being pushed across a frictionless floor with a force of 10 N. What is the net force acting on the box, and what is its acceleration?

In this scenario, the applied force is the net force because there are no other horizontal forces opposing the motion (frictionless surface). Therefore, Fnet = 10 N.

Using Newton’s Second Law, we can calculate the acceleration: a = Fnet / m = 10 N / 5 kg = 2 m/s².

Now let’s increase the complexity. Imagine the same 5 kg box being pulled with a force of 10 N, but this time, there’s a frictional force of 2 N opposing the motion.

What is the net force, and what is the acceleration now?

Here, the net force is the difference between the applied force and the frictional force: Fnet = 10 N – 2 N = 8 N.

The acceleration is then a = Fnet / m = 8 N / 5 kg = 1.6 m/s².

These simple examples demonstrate the direct application of the formula and highlight the importance of considering all forces acting on the object.

Inclined Plane Problems: Introducing Trigonometry

Inclined planes introduce a new layer of complexity because the force of gravity acts at an angle to the surface.

This requires us to resolve the gravitational force into components parallel and perpendicular to the inclined plane.

Consider a block of mass m resting on an inclined plane with an angle θ to the horizontal. The force of gravity (mg) acts vertically downwards.

We need to find the component of gravity acting parallel to the plane (mg sin θ) which causes the block to slide down, and the component acting perpendicular to the plane (mg cos θ), which is balanced by the normal force.

If the block is sliding down the plane with no friction, the net force acting on it is mg sin θ.

The acceleration down the plane is then a = (mg sin θ) / m = g sin θ.

If there is friction, the net force becomes mg sin θ – f, where f is the force of friction. The force of friction is related to the normal force by the equation f = μN, where μ is the coefficient of friction. In this case, the normal force N = mg cos θ.

The resulting acceleration would be a = (mg sin θ – μmg cos θ) / m = g(sin θ – μ cos θ).

These problems require a careful application of trigonometric principles and a clear understanding of how forces are resolved into components.

Multiple Forces in Different Directions: Mastering Vector Addition

The most complex scenarios involve multiple forces acting on an object at different angles. To find the net force in these cases, we must use vector addition.

Vectors have both magnitude and direction, so we can’t simply add them like regular numbers.

The most common method is to resolve each force into its x and y components.

Then, we add the x components together to get the net force in the x direction (Fnet,x) and add the y components together to get the net force in the y direction (Fnet,y).

The magnitude of the net force is then found using the Pythagorean theorem:

Fnet = √(Fnet,x² + Fnet,y²).

The direction of the net force can be found using the arctangent function:

θ = tan⁻¹(Fnet,y / Fnet,x).

For example, imagine a crate being pulled by two ropes. One rope pulls with a force of 50 N at an angle of 30 degrees to the horizontal, and the other pulls with a force of 80 N at an angle of -45 degrees to the horizontal (below the horizontal).

First, resolve the 50 N force into x and y components:
Fx1 = 50 cos(30°) = 43.3 N and Fy1 = 50 sin(30°) = 25 N.

Next, resolve the 80 N force:
Fx2 = 80 cos(-45°) = 56.6 N and Fy2 = 80 sin(-45°) = -56.6 N.

Add the x and y components:
Fnet,x = 43.3 N + 56.6 N = 99.9 N and Fnet,y = 25 N – 56.6 N = -31.6 N.

Finally, calculate the magnitude and direction of the net force:
Fnet = √(99.9² + (-31.6)²) = 104.8 N and θ = tan⁻¹(-31.6 / 99.9) = -17.5°.

Therefore, the net force is approximately 104.8 N at an angle of -17.5 degrees to the horizontal.

The Importance of Accurate Vector Addition

As demonstrated, the process of accurately summing vectors is paramount to calculating the net force when multiple forces are in play. Understanding trigonometry, paying close attention to the direction (sign) of force components, and employing the Pythagorean theorem appropriately are all key. An incorrect vector sum will lead to an incorrect Fnet calculation, in turn, producing an incorrect acceleration calculation. These worked examples should provide a solid foundation for solving more complex and real-world problems involving net force calculations.

Having established the fundamental link between net force and acceleration through Newton’s Second Law, it’s time to ground these abstract concepts in the tangible world. Forces are not just theoretical constructs; they are the invisible hands that shape our daily experiences. Understanding the common types of forces at play allows us to analyze and predict motion in a more intuitive way. Visualizing these forces with tools like Free Body Diagrams further empowers us to understand their effect on an object. Now, let’s translate these diagrams and laws into concrete numerical solutions.

Real-World Applications of Net Force

The study of net force transcends the classroom, offering profound insights into the mechanics of our everyday world. From the mundane to the magnificent, the principles governing net force dictate the behavior of objects in motion and at rest. Let’s examine a few illustrative examples.

Net Force in Motion: The Dynamics of Vehicle Movement

Consider a car accelerating down a highway. The engine generates a forward force, propelling the vehicle forward. However, this is not the only force at play. Friction between the tires and the road opposes this motion, acting as a retarding force. Air resistance, or drag, further complicates the picture.

The net force acting on the car is the vector sum of these individual forces – the engine force, the frictional force, and the aerodynamic drag.

It is this net force that determines the car’s acceleration, dictating how quickly it gains speed. Understanding this interplay of forces is crucial for designing efficient vehicles, optimizing fuel consumption, and ensuring safe driving conditions. When the engine force overcomes both friction and air resistance, the car accelerates. Conversely, if the combined opposing forces exceed the engine force, the car decelerates.

Net Force in Action: Sports and Projectile Motion

The world of sports offers a captivating arena for observing net force in action. Take the example of throwing a baseball. The pitcher applies an external force to the ball, accelerating it to incredible speeds. Once released, however, the pitcher’s force is no longer acting on the ball.

At this point, gravity becomes the dominant force, pulling the ball downwards. Air resistance also plays a significant role, slowing the ball’s horizontal velocity and influencing its trajectory.

The ball’s path, its range, and its ultimate landing point are all determined by the net force acting upon it.

Analyzing these forces is critical in understanding projectile motion, optimizing athletic performance, and designing sports equipment.

Static Equilibrium: Net Force in Construction

The construction industry offers a compelling demonstration of net force in the context of static equilibrium. When a building stands firm, it is in a state of equilibrium, meaning that the net force acting on it is zero.

The weight of the building exerts a downward force due to gravity, while the supporting forces from the foundation counteract this weight, preventing the building from collapsing. Furthermore, external forces such as wind load must also be considered.

Engineers meticulously calculate these forces, ensuring that the supporting structures are robust enough to withstand the anticipated loads. The key principle is that all forces must balance out, resulting in a net force of zero.

Failure to account for these forces can lead to catastrophic consequences. The careful application of net force principles is therefore paramount in ensuring the safety and stability of buildings and infrastructure.

Having explored the applications of net force in various real-world scenarios, it’s crucial to address the common pitfalls that often trip up students and practitioners alike. Understanding the theory is only half the battle; mastering the practical application requires a keen awareness of potential errors and a systematic approach to problem-solving. Let’s delve into these common mistakes and equip you with the strategies to avoid them.

Avoiding Common Mistakes in Net Force Calculations

Successfully navigating net force calculations requires not only a solid grasp of the underlying principles but also an awareness of common pitfalls. Many errors stem from overlooking crucial details, misinterpreting the problem setup, or simply making algebraic mistakes. By identifying these potential issues, we can develop strategies to sidestep them and ensure accurate results.

The Overlooked Force: Identifying All Players

One of the most frequent errors is failing to identify all the forces acting on an object. It’s easy to focus on the obvious forces, like applied forces or gravity, but often, subtle forces like friction, air resistance, or tension are overlooked.

Remember, the net force is the vector sum of all forces.

Leaving out even one force will lead to an incorrect result.

To avoid this, start by drawing a thorough free body diagram. Systematically list every object interacting with the object of interest and identify the force it exerts. Double-check for any hidden or implied forces.

Direction Matters: Vector Addition and Sign Conventions

Force is a vector quantity, meaning it has both magnitude and direction. A common mistake is treating forces as simple numbers and adding them algebraically without considering their directions. This is particularly problematic when forces act at angles or in opposing directions.

Sign Conventions Are Key

Establish a clear sign convention (e.g., rightward and upward forces are positive, leftward and downward forces are negative) and consistently apply it throughout the problem. Use trigonometric functions (sine, cosine, tangent) to resolve forces into their horizontal and vertical components before adding them.

Vector addition is crucial for accurately determining the net force. For example, if a box is pushed to the right with 10 N and friction exerts 3 N to the left, the net horizontal force is 10 N – 3 N = 7 N to the right, not 13 N.

Unit Conversion and Dimensional Consistency

Another frequent source of error is neglecting to use consistent units. The net force formula, Fnet = ma, requires that mass be in kilograms (kg), acceleration in meters per second squared (m/s²), and force in Newtons (N).

If the mass is given in grams or the acceleration in kilometers per hour squared, you must convert them to the appropriate units before plugging them into the formula.

Dimensional Analysis

Always perform dimensional analysis to check that your units are consistent throughout the calculation. This means ensuring that the units on both sides of the equation match.

For example, if you’re calculating force and end up with units of kg m/s, you know something went wrong. The correct unit for force is Newtons (N), which is equivalent to kg m/s². Catching these inconsistencies early can save you from making significant errors.

And that’s the net force formula in a nutshell! Hopefully, you now feel much more comfortable tackling problems involving forces. Keep practicing, and you’ll be a pro in no time. Good luck!