Hemisphere Area Formula: The Only Guide You’ll Ever Need

Understanding the hemisphere area formula is foundational for success in fields leveraging geometry. Specifically, calculating surface area, particularly for spherical sections, is crucial in this. The applications extend into sectors managed by organizations like NASA, especially in space vehicle design. Even further, knowledge of the hemisphere area formula is instrumental in computational fluid dynamics modeling, championed in the work of researchers at the National Institute of Standards and Technology (NIST). It equips professionals using CAD software to model structures accurately, making design processes more precise. Therefore, the hemisphere area formula is not just a theoretical concept; it’s a practical tool with diverse applications.

Welcome to the fascinating realm of three-dimensional shapes and geometric principles! This guide will serve as your compass, navigating you through the intricacies of calculating the surface area of a hemisphere.

Geometry, at its core, is the study of shapes, sizes, relative positions of figures, and the properties of space. Within this vast discipline lies a subset focused on three-dimensional objects, adding depth and volume to the familiar two-dimensional landscape.

A Glimpse into 3D Shapes and Geometry

Three-dimensional (3D) shapes inhabit the world around us. From the pyramids of Giza to the intricate designs of modern architecture, 3D geometry plays a vital role in both aesthetics and functionality.

Geometry is not just about memorizing formulas. It is about understanding the relationships between different elements and how they come together to define the characteristics of a shape.

Spheres and Hemispheres: Defining the Terms

Before we dive into the specifics of the hemisphere area formula, let’s clarify what exactly constitutes a sphere and a hemisphere.

A sphere is a perfectly round geometrical object in three-dimensional space. Think of a basketball or a perfectly round globe.

A hemisphere, quite simply, is exactly one-half of a sphere. Imagine taking a sphere and slicing it perfectly in half; each resulting piece is a hemisphere. The Earth itself can be divided into the Northern and Southern Hemispheres.

Understanding these fundamental definitions is crucial for grasping the formula we are about to explore.

Why Understanding the Hemisphere Area Formula Matters

Why dedicate time and effort to understanding the hemisphere area formula? The answer lies in its practical applications and its contribution to problem-solving skills.

Calculating the surface area of a hemisphere is not merely an academic exercise. It has tangible applications in diverse fields like engineering, architecture, and even culinary arts (think of hemispherical cake molds!).

Moreover, mastering this formula reinforces your understanding of geometric principles and enhances your ability to approach and solve complex spatial problems.

Purpose of This Guide: A Comprehensive Exploration

This guide is designed to provide you with a comprehensive and accessible understanding of the hemisphere area formula.

We will not just present you with the formula; we will dissect it, explain its components, demonstrate its applications, and equip you with the tools to confidently use it in various scenarios.

By the end of this guide, you will possess a solid understanding of:

• The foundational concepts that underpin the formula.
• The formula itself and its derivation.
• Step-by-step methods for applying the formula correctly.
• Real-world applications of the hemisphere area formula.

Whether you are a student, a professional, or simply a curious mind, this guide will empower you with the knowledge and skills to confidently tackle any hemisphere-related area calculation.

Why dedicate time and effort to understanding the area of a hemisphere? The answer lies in its widespread relevance, from architecture and engineering to everyday life. Before we can confidently tackle the formula itself, it’s essential to solidify our understanding of a few key foundational concepts. These building blocks will provide the context and clarity needed to truly grasp the hemisphere area formula and its significance.

Foundational Concepts: Building Blocks of Understanding

To truly understand the surface area of a hemisphere, we must first revisit some essential geometric concepts. These include understanding the properties of a circle, the significance of Pi (π), and the fundamental characteristics of a sphere itself. Let’s delve into these concepts.

The Ubiquitous Circle

The circle serves as the cornerstone for understanding spheres and hemispheres. After all, slicing a sphere results in circular cross-sections.

Understanding the circle is crucial because it forms the very basis for defining the radius and ultimately calculating the surface area.

Radius and Diameter: Defining Circular Dimensions

Two primary measurements define a circle: the radius (r) and the diameter.

The radius is the distance from the center of the circle to any point on its edge.

The diameter, on the other hand, is the distance across the circle passing through its center.

Notably, the diameter is always twice the length of the radius (d = 2r). This simple relationship becomes essential when working with hemisphere calculations, as you might be given either the radius or the diameter in a problem.

Pi (π): The Unending Constant

Pi (π) is a mathematical constant representing the ratio of a circle’s circumference to its diameter. It is approximately equal to 3.14159, although its decimal representation continues infinitely without repeating.

Pi is an irrational number, meaning it cannot be expressed as a simple fraction.

Its ubiquitous presence in geometry and other branches of mathematics is undeniable, and understanding its significance is critical when calculating the area of any shape involving circular elements, including hemispheres. Without Pi, calculating areas and volumes of circular shapes would be impossible.

Spheres and Hemispheres: A Three-Dimensional Perspective

A sphere is a perfectly round three-dimensional object, where every point on its surface is equidistant from its center. Think of a ball or a globe.

A hemisphere, as previously mentioned, is simply one-half of a sphere.

Imagine cutting a sphere perfectly in half, and each resulting piece is a hemisphere.

Understanding the relationship between a sphere and a hemisphere is crucial. The curved surface of a hemisphere is exactly half the surface area of its corresponding sphere. However, the total surface area of a hemisphere includes the circular base created by the cut. This distinction is key to applying the correct formula, as we will explore later.

The Hemisphere Area Formula: Decoding the Equation

Having established the foundational geometric principles, we can now directly address the core of our exploration: the hemisphere area formula. It’s more than just a mathematical expression.

It’s a powerful tool for understanding and quantifying the surface of this ubiquitous three-dimensional shape. Let’s break down the equation, understand its components, and reveal its derivation.

Unveiling the Hemisphere’s Surface Area Formulas

A hemisphere, essentially half a sphere, presents a unique challenge when calculating its surface area. This is because we have two distinct surface area measurements to consider: the curved surface area and the total surface area.

Understanding the distinction between these two is crucial for accurate calculations and real-world applications.

The curved surface area refers solely to the rounded exterior of the hemisphere. In contrast, the total surface area includes the curved surface area plus the circular base.

Therefore, we have two formulas at our disposal:

• Total Surface Area (A) = 3πr²
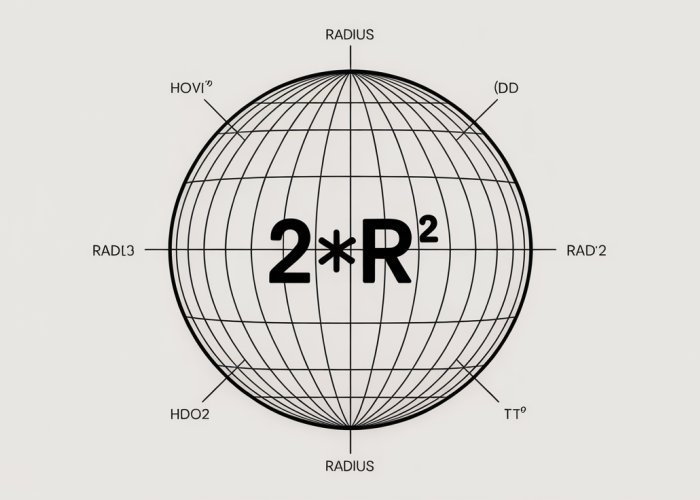
• Curved Surface Area (A) = 2πr²

Where "A" represents the area and "r" represents the radius of the hemisphere.

Dissecting the Formula’s Components

At first glance, the hemisphere area formulas may appear straightforward. However, understanding each component is key to truly mastering their application.

Let’s examine the individual elements that contribute to the final calculation:

Pi (π): The Constant of Circularity

As previously established, Pi (π) is a fundamental mathematical constant representing the ratio of a circle’s circumference to its diameter. It is approximately equal to 3.14159.

Its presence in the hemisphere area formula underscores the inherent connection between circles and spheres. It’s an irrational number.

This means its decimal representation neither terminates nor repeats. In practical calculations, we often use approximations like 3.14 or 22/7.

Radius (r): Defining the Hemisphere’s Size

The radius (r) is the distance from the center of the circular base of the hemisphere to any point on its edge. As discussed earlier, it’s half the diameter.

The radius is arguably the most important variable in the formula, as it directly determines the size and, consequently, the surface area of the hemisphere.

A larger radius translates to a significantly larger surface area, as the area increases proportionally to the square of the radius.

Tracing the Formula’s Origins: Connecting to the Sphere

The hemisphere area formula isn’t arbitrary. It’s directly derived from the surface area formula of a complete sphere. The surface area of a sphere is given by the formula 4πr².

Intuitively, one might expect the curved surface area of a hemisphere to be simply half of this, or 2πr². And indeed, that is precisely the formula for the curved surface area.

The total surface area of the hemisphere (3πr²) includes the area of the circular base (πr²) created when the sphere is divided in half. This addition accounts for the extra surface, giving the total surface area.

Thus, by understanding the relationship between the sphere and the hemisphere, we gain a deeper appreciation for the logic and elegance of the formula. It connects the two shapes.

Step-by-Step Calculation Guide: Mastering the Formula

Having dissected the formula’s components, it’s time to put our knowledge into practice. This section provides a practical, step-by-step guide to calculating the surface area of a hemisphere, ensuring you can confidently apply the formula in various scenarios. We’ll work through example problems and highlight common pitfalls to help you master this essential geometric calculation.

Calculating Hemisphere Surface Area: A Step-by-Step Approach

To effectively calculate the surface area of a hemisphere, whether it’s the curved surface area or the total surface area, follow these steps:

1. Identify the Radius (r): The most crucial piece of information is the radius of the hemisphere. This is the distance from the center of the circular base to any point on the circumference.

2. Choose the Correct Formula: Determine whether you need to calculate the curved surface area (A = 2πr²) or the total surface area (A = 3πr²). Carefully consider the problem’s context to select the appropriate formula.

3. Substitute the Radius Value: Replace the ‘r’ in the chosen formula with the known radius value.

4. Calculate πr²: First, square the radius (r²), and then multiply the result by π (approximately 3.14159).

5. Multiply by the Coefficient: Multiply the result from the previous step by either 2 (for curved surface area) or 3 (for total surface area).

6. State the Units: Ensure you include the correct units for area (e.g., square meters, square inches). The units are just as important as the numerical answer.

Example Problem 1: Calculating the Area Given the Radius (r)

Let’s say we have a hemisphere with a radius of 5 cm and we want to find the total surface area.

1. Radius (r): r = 5 cm
2. Formula: A = 3πr² (Total Surface Area)
3. Substitution: A = 3π(5 cm)²
4. Calculate πr²: (5 cm)² = 25 cm², then 25 cm²

   **π ≈ 78.54 cm²

5. Multiply: A ≈ 3** 78.54 cm² ≈ 235.62 cm²
6. Units: The total surface area is approximately 235.62 square centimeters.

Therefore, the total surface area of the hemisphere is approximately 235.62 cm².

Example Problem 2: Calculating the Area Given the Diameter

Suppose you’re given a hemisphere with a diameter of 12 inches, and you need to determine its curved surface area.

1. Diameter: d = 12 inches. Therefore, the Radius (r) = d/2 = 6 inches.
2. Formula: A = 2πr² (Curved Surface Area)
3. Substitution: A = 2π(6 inches)²
4. Calculate πr²: (6 inches)² = 36 inches², then 36 inches²

   **π ≈ 113.10 inches²

5. Multiply: A ≈ 2** 113.10 inches² ≈ 226.20 inches²
6. Units: The curved surface area is approximately 226.20 square inches.

Thus, the curved surface area of the hemisphere is approximately 226.20 in².

Common Mistakes and How to Avoid Them

Even with a clear understanding of the formula, errors can occur. Here’s how to avoid some common mistakes:

• Confusing Radius and Diameter: Always double-check whether you’re given the radius or the diameter. If you’re given the diameter, remember to divide it by 2 to find the radius.

• Using the Wrong Formula: Make sure you’re using the correct formula for either the curved surface area (2πr²) or the total surface area (3πr²). Carefully read the problem to determine what is being asked.

• Forgetting Units: Always include the appropriate units (e.g., cm², m², in²) in your final answer. Omitting units can lead to misinterpretations.

• Rounding Errors: Avoid rounding intermediate calculations too early, as this can affect the accuracy of your final answer. Keep at least four decimal places during calculations and round only at the end.

• Misunderstanding Order of Operations: Make sure to square the radius before multiplying by Pi and the coefficient (2 or 3). Follow the standard order of operations (PEMDAS/BODMAS).

By following these guidelines and practicing with various examples, you’ll be well-equipped to accurately calculate the surface area of any hemisphere you encounter.

Real-World Applications: Where Hemispheres Come to Life

Having mastered the step-by-step calculation of hemisphere surface area, you might be wondering, "Where does all this geometry actually get used?" The truth is, hemispheres and their surface area calculations pop up in a surprising number of places, from the architecture around us to the tools scientists use every day. Understanding these applications helps solidify the importance of the formula and reveals how theoretical knowledge translates into practical solutions.

Architectural Marvels: Domes and Beyond

One of the most visually striking applications of hemispheres is in architecture, particularly in the construction of domes.

Domes are efficient structures that can cover large areas without the need for internal supports.

The surface area calculation is critical for determining the amount of material needed to build the dome, whether it’s concrete, glass, or another material.

Consider iconic structures like the Pantheon in Rome or modern geodesic domes. Accurate surface area calculations are vital for cost estimation, structural integrity, and even thermal performance.

Industrial Solutions: Tanks and Storage

Hemispherical shapes are also common in industrial applications, particularly in the design of tanks and storage vessels.

The rounded shape of a hemisphere offers strength and efficient volume containment.

Large tanks designed to hold liquids or gases often incorporate hemispherical ends or tops.

Calculating the surface area is essential for determining the amount of material needed for construction.

It also aids in calculating the amount of insulation required to maintain the contents at a specific temperature. This is particularly important in industries dealing with cryogenic liquids or volatile chemicals.

Scientific Instruments: Precision and Accuracy

Beyond architecture and industry, hemispheres play a crucial role in scientific instrumentation.

Many types of lenses, reflectors, and sensors utilize hemispherical shapes to maximize light gathering or signal reception.

For example, certain types of telescopes or specialized microscopes incorporate hemispherical lenses.

The accuracy of these instruments often depends on the precise dimensions and surface area of the hemispherical components.

Surface area calculations help to determine the reflective or refractive properties.

This allows scientists to accurately interpret data and conduct experiments.

Everyday Examples: A World of Hemispheres

While the examples above showcase large-scale applications, it’s worth noting that hemispheres are also present in many everyday objects.

Think of the bowl of a spoon, the cap of a pen, or even the dome-shaped lid of a container.

While we may not consciously calculate their surface areas, these shapes offer advantages in terms of functionality, aesthetics, and structural integrity.

The underlying geometric principles remain the same, regardless of the scale.

The Power of Geometric Knowledge

These real-world examples highlight the power of geometry in solving practical problems.

The hemisphere area formula isn’t just an abstract mathematical concept.

It’s a tool that engineers, architects, and scientists use to design, build, and understand the world around us.

By understanding the principles behind the formula, you gain a deeper appreciation for the role of mathematics in shaping our environment and advancing human knowledge.

Advanced Topics (Optional): Delving Deeper into Geometry

Having explored the practical applications of the hemisphere area formula, let’s venture into more advanced geometrical territories. This section is designed for those with a keen interest in the theoretical underpinnings and broader connections within the world of mathematics.

We will explore how the hemisphere area formula relates to other geometric concepts and touch upon the role of calculus in its derivation. This is an optional but rewarding journey for those seeking a deeper understanding.

Hemispheres and Their Geometric Kin: A Network of Relationships

The hemisphere area formula doesn’t exist in isolation. It’s part of a web of interconnected geometric ideas. Understanding these connections can enrich your comprehension of the formula itself.

The Sphere: A Foundation

The most obvious connection is to the sphere itself. The hemisphere, by definition, is half a sphere.

The surface area of a sphere is 4πr², and a hemisphere’s curved surface is precisely half of that (2πr²). The total surface area of a hemisphere includes the circular base, adding another πr² to the curved surface area.

This direct relationship highlights the foundational role of the sphere in understanding the hemisphere’s properties.

Cylinders: An Intriguing Link

There’s a fascinating relationship between a hemisphere and a cylinder with the same radius and height (equal to the radius). Imagine fitting a hemisphere snugly inside such a cylinder.

The curved surface area of the cylinder (excluding the top and bottom) is 2πrh, which, since h = r, becomes 2πr². This is equal to the curved surface area of the hemisphere.

This equivalence is not merely a coincidence; it reflects deeper geometric principles related to surface area and volume.

Cones: A More Distant Cousin

While not as directly related as spheres or cylinders, cones share geometrical similarities with hemispheres, especially in concepts of volume calculation and surface generation.

Exploring the ratios and relationships between these shapes can offer valuable insights into spatial reasoning.

Calculus and the Hemisphere: A Derivation Perspective

While we provided the formula earlier, it’s worthwhile to briefly consider how calculus can be used to derive the surface area of a hemisphere.

This approach involves integration and provides a more rigorous mathematical justification for the formula.

Surface of Revolution

One common calculus approach involves treating the hemisphere as a surface of revolution.

Imagine rotating a semicircle around an axis. The resulting 3D shape is a hemisphere. Calculus allows us to calculate the surface area generated by this rotation using integration.

The Integral Setup

The surface area can be found by integrating the infinitesimal arc length along the semicircle, multiplied by the circumference of the circle traced by that arc length as it rotates.

This integral yields the familiar 2πr² for the curved surface area of the hemisphere.

Why Calculus Matters

While not essential for basic calculations, understanding the calculus-based derivation provides a deeper appreciation for the formula’s origins.

It showcases the power of calculus in solving geometric problems and highlights the interconnectedness of different mathematical disciplines.

Alright, you’ve now got a handle on the hemisphere area formula! Time to go forth and conquer those geometry problems. Hope this makes figuring it all out a little easier! Keep practicing!