Unlock Atomic Secrets: Energy Sub Levels Explained!

Quantum mechanics, a cornerstone of modern physics, provides the framework for understanding the energy sub level, the central concept in atomic structure. The Schrödinger equation, a key tool for calculating atomic energy levels, reveals how electrons occupy specific energy states within atoms. These states are influenced by the Pauli exclusion principle, a fundamental rule that governs electron configuration and distribution. Consequently, the arrangement of electrons within each energy sub level dictates the chemical properties of elements, information that is vital to research done at places like CERN and other facilities around the world. Understanding energy sub level configurations is key to deciphering the behaviors of atoms and molecules.

Have you ever stopped to consider that the vibrant colors of a sunset, the intricate workings of a solar panel, and the very structure of your own body are all governed by the behavior of tiny particles within atoms? It’s a profound thought, isn’t it? This seemingly invisible world dictates the properties of everything we see and interact with.

The Significance of Energy Levels

At the heart of this atomic realm lies the concept of energy levels. Understanding these levels is not just an exercise in theoretical physics; it is crucial for comprehending how atoms interact to form molecules, how chemical reactions occur, and why materials possess the properties they do.

Think of it this way: atoms are the building blocks of matter, and energy levels are the blueprints that dictate how those blocks can be assembled. Without grasping the intricacies of energy levels, we are left with only a superficial understanding of the universe around us.

Exploring the Atomic Structure

This article aims to delve into the fascinating world of energy sublevels, the subdivisions within the main energy levels that add a layer of complexity and nuance to atomic behavior. We will explore their connections to atomic orbitals, those elusive regions of space where electrons are most likely to be found.

Furthermore, we’ll unravel the significance of quantum numbers, the unique identifiers that describe the state of each electron within an atom. Finally, we will discuss how all of these concepts come together in the electron configuration, the roadmap that dictates how electrons arrange themselves to create a stable atom.

Through this exploration, we hope to provide a comprehensive view of atomic structure and equip you with the knowledge necessary to appreciate the underlying principles that govern the material world.

Have you ever stopped to consider that the vibrant colors of a sunset, the intricate workings of a solar panel, and the very structure of your own body are all governed by the behavior of tiny particles within atoms? It’s a profound thought, isn’t it? This seemingly invisible world dictates the properties of everything we see and interact with.

The Significance of Energy Levels

At the heart of this atomic realm lies the concept of energy levels. Understanding these levels is not just an exercise in theoretical physics; it is crucial for comprehending how atoms interact to form molecules, how chemical reactions occur, and why materials possess the properties they do.

Think of it this way: atoms are the building blocks of matter, and energy levels are the blueprints that dictate how those blocks can be assembled. Without grasping the intricacies of energy levels, we are left with only a superficial understanding of the universe around us.

The atom’s composition and behavior may feel like a complicated enigma, but the principles governing atomic structure begin with a fundamental idea: Energy levels. These levels establish the framework for atomic behavior and dictate the properties of matter. Let’s take a closer look at this essential element.

Energy Levels: The Foundation of Atomic Structure

The realm within the atom, though unseen, operates under precise rules. Perhaps the most fundamental of these rules is the quantization of energy.

Electrons, those negatively charged particles orbiting the nucleus, can only exist at specific, discrete energy levels.

Quantized Energy States

Imagine a staircase: you can stand on one step or another, but never in between. Similarly, electrons can only occupy certain energy levels within an atom.

These levels are not continuous; they are quantized, meaning they come in specific, defined amounts. This quantization is a cornerstone of quantum mechanics.

Each energy level corresponds to a specific amount of energy that an electron must possess to reside in that level. The further the energy level from the nucleus, the higher its energy.

Electrons and Energy Level Occupation

Electrons cannot simply exist with any arbitrary amount of energy. They are restricted to these defined energy states.

An electron in the lowest energy level is said to be in its ground state.

If an electron absorbs energy, such as from a photon of light, it can jump to a higher energy level, becoming excited. However, this excited state is unstable.

The electron will eventually return to a lower energy level, releasing the excess energy as a photon of light. This process is the basis for many phenomena, including the emission of light from neon signs and the colors of fireworks.

Introducing Energy Sublevels

While the concept of distinct energy levels provides a crucial foundation, the story doesn’t end there. Each main energy level is further divided into energy sublevels.

These sublevels introduce a new layer of complexity and nuance to atomic behavior.

These sublevels are designated by the letters s, p, d, and f. Each sublevel has a slightly different energy within the main energy level.

For example, the second energy level (n=2) contains two sublevels: the 2s sublevel and the 2p sublevel. The existence of sublevels explains the finer details observed in atomic spectra and chemical bonding.

Understanding energy sublevels is crucial for predicting how atoms will interact with each other to form molecules and materials.

Electrons, those negatively charged particles orbiting the nucleus, can only exist at specific, discrete energy levels. These energy levels, however, are not monolithic. They possess a finer structure, subdividing into what we call energy sublevels. Understanding this unlocks a deeper appreciation of how atoms truly behave.

Atomic Orbitals: Visualizing Electron Probability

The concept of energy sublevels naturally leads us to the fascinating realm of atomic orbitals. These orbitals aren’t simply fixed paths like planets orbiting a star. Instead, they represent something far more nuanced: regions of probability.

Defining Atomic Orbitals

An atomic orbital is best defined as a three-dimensional region of space around the nucleus of an atom where there is a high probability of finding an electron. It’s not a precise location, but rather a map of likelihood.

Think of it like this: if you were to repeatedly measure the position of an electron in an atom, and then plot all those positions on a graph, the resulting shape would resemble the atomic orbital. The denser the cloud of points, the higher the probability of finding the electron in that region.

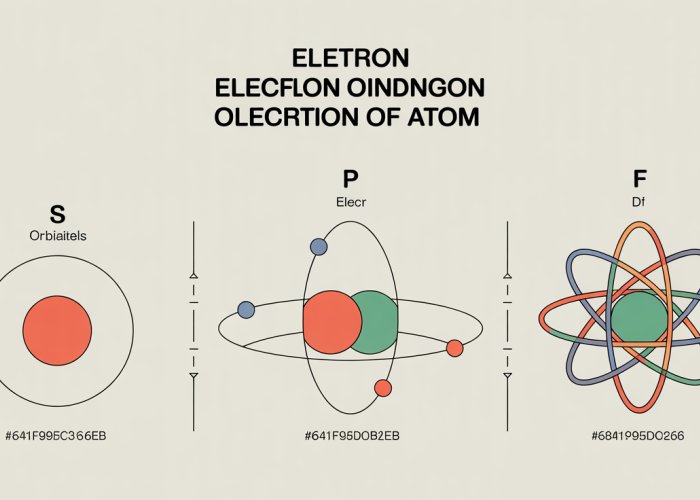
The Shapes of Atomic Orbitals: s, p, d, and f

Atomic orbitals come in a variety of shapes, each corresponding to a specific energy sublevel. The most common types are designated as s, p, d, and f.

s Orbitals: Spherical Symmetry

The s orbitals are the simplest in shape, possessing a spherical symmetry around the nucleus. This means the probability of finding the electron is the same in all directions at a given distance from the nucleus.

There is only one s orbital per energy level. As the principal quantum number (n) increases (n=1, 2, 3…), the size of the s orbital also increases, indicating that the electron is more likely to be found farther away from the nucleus.

p Orbitals: Dumbbell-Shaped

The p orbitals are more complex, resembling dumbbells or figure-eights. Unlike s orbitals, p orbitals have directional properties.

There are three p orbitals per energy level (starting with n=2), oriented along the x, y, and z axes. These are often denoted as px, py, and pz.

The electron density is concentrated in two lobes on either side of the nucleus, with a node (a region of zero electron density) at the nucleus itself.

d Orbitals: More Complex Geometries

The d orbitals are even more intricate in shape than p orbitals. Most d orbitals have four lobes, although one has a dumbbell shape with a ring around it.

There are five d orbitals per energy level (starting with n=3), each with a unique spatial orientation. Visualizing these orbitals can be challenging, but understanding their shapes is crucial for comprehending the bonding properties of transition metals.

f Orbitals: Highly Complex and Diffuse

The f orbitals are the most complex and diffuse of the common atomic orbitals. Their shapes are difficult to depict and visualize.

There are seven f orbitals per energy level (starting with n=4). They play a significant role in the chemistry of lanthanides and actinides.

The Relationship Between Energy Sublevels and Atomic Orbitals

There is a direct and fundamental relationship between energy sublevels and the types of atomic orbitals. Each energy sublevel corresponds to a specific type and number of atomic orbitals:

• The s sublevel corresponds to one s orbital.
• The p sublevel corresponds to three p orbitals.
• The d sublevel corresponds to five d orbitals.
• The f sublevel corresponds to seven f orbitals.

This relationship is not arbitrary; it’s dictated by the solutions to the Schrödinger equation, the cornerstone of quantum mechanics. The quantum numbers that arise from solving this equation determine the shape, energy, and spatial orientation of each atomic orbital.

By understanding atomic orbitals, we gain a powerful tool for visualizing the probability distribution of electrons within an atom. This understanding is essential for predicting and explaining chemical bonding, molecular properties, and the behavior of matter at the atomic level.

Atomic orbitals, with their diverse shapes and spatial orientations, provide a visual representation of where electrons reside. But to truly pinpoint the identity of an electron within an atom, we need a more precise system: quantum numbers. These numbers act like a unique address, defining the specific state of each electron and providing a complete picture of its properties.

Quantum Numbers: Defining Electron Identity

Think of quantum numbers as a set of coordinates that pinpoint the precise location and characteristics of each electron within an atom. Just as a street address identifies a specific house, quantum numbers identify a specific electron.

There are four quantum numbers in total, each providing a crucial piece of information: the Principal Quantum Number (n), the Azimuthal Quantum Number (l), the Magnetic Quantum Number (ml), and the Spin Quantum Number (ms). Let’s examine each of these in detail.

The Principal Quantum Number (n): Energy Level

The Principal Quantum Number (n) is perhaps the most intuitive. It defines the energy level, or electron shell, that an electron occupies.

This number is always a positive integer (n = 1, 2, 3, and so on). Higher values of n indicate higher energy levels and greater average distance from the nucleus.

You can relate this to the Bohr model of the atom, where electrons orbit the nucleus in specific, quantized paths or shells. Each shell corresponds to a specific value of n. For instance, n = 1 represents the innermost shell, closest to the nucleus, and is often called the ground state.

The Azimuthal Quantum Number (l): Orbital Shape

The Azimuthal Quantum Number (l), also known as the angular momentum quantum number, determines the shape of the atomic orbital. It also reveals the energy sublevel within a given principal energy level.

The value of l can range from 0 to n-1. Each value of l corresponds to a specific orbital shape:

• l = 0 corresponds to an s orbital, which is spherical.

• l = 1 corresponds to a p orbital, which is dumbbell-shaped.

• l = 2 corresponds to a d orbital, which has more complex shapes.

• l = 3 corresponds to an f orbital, which has even more intricate shapes.

Crucially, the Azimuthal Quantum Number establishes a direct link between energy sublevels (s, p, d, f) and the corresponding shapes of atomic orbitals. The shape directly influences how the electron interacts with other atoms, and how chemical bonds are formed.

The Magnetic Quantum Number (ml): Spatial Orientation

The Magnetic Quantum Number (ml) specifies the orientation of the atomic orbital in space. For a given value of l, ml can take on integer values from –l to +l, including 0.

This means that an s orbital (l = 0) has only one possible orientation (ml = 0) because it is spherical. A p orbital (l = 1), however, has three possible orientations (ml = -1, 0, +1), corresponding to the three p orbitals oriented along the x, y, and z axes.

The spatial orientation of an orbital becomes particularly important when atoms interact to form molecules.

The Spin Quantum Number (ms): Electron Spin

Finally, the Spin Quantum Number (ms) describes the intrinsic angular momentum of an electron, also known as its spin. Electrons behave as if they are spinning, creating a magnetic dipole moment.

This spin is quantized, meaning it can only have two possible orientations: spin up or spin down. These are assigned the values of +1/2 and -1/2, respectively. The direction of electron spin affects its magnetic properties and how it interacts with external magnetic fields.

The Quantum Number Combination

The power of quantum numbers lies in their combination. Together, these four numbers uniquely define the state of an electron within an atom.

No two electrons in the same atom can have the same set of all four quantum numbers (Pauli Exclusion Principle).

This principle dictates how electrons fill energy levels and sublevels, leading to the diverse chemical properties observed in the periodic table. By understanding the possible combinations of quantum numbers, we can predict the electronic structure of atoms and the types of chemical bonds they are likely to form. The n, l, ml, and ms values dictate electron behavior and define the very identity of each electron within an atom.

Atomic orbitals, with their diverse shapes and spatial orientations, provide a visual representation of where electrons reside. But to truly pinpoint the identity of an electron within an atom, we need a more precise system: quantum numbers. These numbers act like a unique address, defining the specific state of each electron and providing a complete picture of its properties.

Electron Configuration: Building Atoms Electron by Electron

Having established the framework of quantum numbers and their influence on electron behavior, we can now explore how these principles dictate the actual arrangement of electrons within an atom. This arrangement, known as the electron configuration, governs an atom’s chemical properties and its interactions with other atoms.

Defining Electron Configuration

Electron configuration describes the specific distribution of electrons among the various energy levels and sublevels within an atom. It’s a shorthand notation that reveals which orbitals are occupied and how many electrons each orbital contains.

Understanding electron configuration is essential for predicting an atom’s reactivity, its bonding behavior, and its overall place within the periodic table. It acts as a blueprint for understanding the chemical world.

The Aufbau Principle: Filling Orbitals Systematically

The Aufbau principle, derived from the German word for "building up," provides a systematic approach to determining the electron configuration of an atom.

It dictates that electrons first occupy the lowest energy levels and sublevels available before filling higher energy ones. This principle helps us predict the order in which electrons will populate the atomic orbitals.

The Aufbau principle isn’t a rigid rule, but rather a guideline. The energy levels of orbitals can sometimes shift depending on the specific atom and the interactions between its electrons.

Visualizing the Aufbau Principle: The (n+l) Rule

A helpful mnemonic for remembering the order of orbital filling is the (n+l) rule. This rule states that orbitals with lower (n+l) values are filled first. If two orbitals have the same (n+l) value, the orbital with the lower n value is filled first.

For example, the 4s orbital (n=4, l=0, n+l=4) is filled before the 3d orbital (n=3, l=2, n+l=5), even though the 4s orbital has a higher principal quantum number.

Hund’s Rule and the Pauli Exclusion Principle: Fine-Tuning the Arrangement

While the Aufbau principle provides a general framework for filling orbitals, two additional rules refine the process and ensure that the electron configuration is both stable and accurate: Hund’s Rule and the Pauli Exclusion Principle.

Hund’s Rule: Maximizing Multiplicity

Hund’s Rule states that within a given subshell (e.g., p, d, or f), electrons will individually occupy each orbital before any one orbital is doubly occupied.

Furthermore, these singly occupied orbitals will have the same spin (either all spin up or all spin down) to minimize electron-electron repulsion. This maximizes the total spin angular momentum and results in a more stable electron configuration.

The Pauli Exclusion Principle: No Identical Electrons

The Pauli Exclusion Principle is a fundamental principle of quantum mechanics that dictates that no two electrons in an atom can have the same set of four quantum numbers.

This means that each electron must have a unique "address" defined by its principal quantum number (n), azimuthal quantum number (l), magnetic quantum number (ml), and spin quantum number (ms).

Consequently, each atomic orbital can hold a maximum of two electrons, and these two electrons must have opposite spins (+1/2 and -1/2).

In essence, the Pauli Exclusion Principle sets the limit on how many electrons can occupy a specific region of space, and provides the physical basis for the structure of the periodic table.

Having mastered the rules governing the electron configuration within an atom, a natural question arises: how do we know all of this is true? How do we experimentally verify these theoretical models of atomic structure? The answer lies in a powerful set of techniques known collectively as spectroscopy.

Spectroscopy: Peering into Atomic Energy Levels Through Light

Spectroscopy provides a crucial bridge between theoretical models of atomic structure and experimental observations. It allows scientists to probe the intricate energy levels within atoms by analyzing the light they absorb or emit.

The Essence of Spectroscopy

At its core, spectroscopy is an experimental technique that investigates the interaction of electromagnetic radiation (light) with matter. In the context of atomic structure, it’s used to precisely determine the energy levels within atoms. This is achieved by carefully analyzing the wavelengths (or frequencies) of light that atoms absorb or emit.

Absorption and Emission: Electron Transitions

The foundation of spectroscopy rests on the principle that electrons can transition between energy levels within an atom. When an electron moves from a lower energy level to a higher one, it must absorb energy equal to the energy difference between the two levels. This energy is typically supplied by a photon of light.

Conversely, when an electron transitions from a higher energy level to a lower one, it emits a photon of light with an energy equal to the energy difference. These absorption and emission events are highly specific. An atom will only absorb or emit photons with energies that exactly match the energy differences between its allowed energy levels.

Quantifying the Light: ΔE = hν

The relationship between the energy of the photon (E) and its frequency (ν) is described by the equation:

ΔE = hν

where h is Planck’s constant. This equation is fundamental to understanding spectroscopy. It demonstrates that the energy of the absorbed or emitted photon directly corresponds to the energy difference (ΔE) between the initial and final energy levels of the electron. By measuring the frequency (or wavelength) of the light, scientists can precisely determine these energy differences.

Types of Spectroscopic Techniques

Spectroscopy encompasses a wide array of techniques, each tailored to specific applications and regions of the electromagnetic spectrum. Two common types are:

• Absorption Spectroscopy: In this technique, a beam of light is passed through a sample of atoms. By analyzing which wavelengths of light are absorbed, scientists can identify the energy levels within the atoms. Dark lines appear in the spectrum at wavelengths corresponding to absorbed photons.

• Emission Spectroscopy: Here, atoms are excited to higher energy levels, typically by heating them or passing an electric discharge through them. As the excited atoms return to their ground state, they emit photons of light. The emitted light is then analyzed to determine the wavelengths and intensities of the emitted photons, revealing the atom’s energy levels. Bright lines appear in the spectrum at wavelengths corresponding to emitted photons.

These techniques, and many others within the broader field of spectroscopy, provide invaluable insights into the quantized world of atomic energy levels, allowing us to experimentally validate and refine our theoretical understanding of atomic structure.

Spectroscopy offers compelling evidence for the quantized nature of atomic energy levels. But to truly grasp why these levels exist and why electrons behave as they do within atoms, we need to delve into the realm of quantum mechanics.

Quantum Mechanics: The Foundation of Atomic Behavior

Quantum mechanics isn’t just a set of rules; it’s a fundamental theory that reshaped our understanding of the universe at the smallest scales. It provides the theoretical framework upon which our understanding of energy levels, atomic orbitals, and even electron spin is built.

The Quantum Revolution

Classical physics, which accurately describes the motion of everyday objects, fails spectacularly when applied to atoms and subatomic particles.

Quantum mechanics emerged in the early 20th century to address these shortcomings, introducing revolutionary concepts like quantization, wave-particle duality, and the uncertainty principle.

At its core, quantum mechanics posits that energy, momentum, and other physical quantities are not continuous but exist in discrete, quantized values.

This quantization is what gives rise to the distinct energy levels observed in atoms.

Predicting Quantized Energy Levels and Atomic Orbitals

One of the most profound achievements of quantum mechanics is its ability to predict the existence and properties of quantized energy levels and atomic orbitals.

The Schrödinger equation, a cornerstone of quantum mechanics, describes the behavior of electrons in atoms. Solving this equation for a given atom yields a set of solutions that correspond to the allowed energy levels and the shapes of the atomic orbitals.

These solutions reveal that electrons can only exist in specific energy states, and that these states are associated with particular spatial distributions, the atomic orbitals.

The s, p, d, and f orbitals, with their characteristic shapes, are not arbitrary constructs but rather direct consequences of the mathematical solutions to the Schrödinger equation. Quantum mechanics explains why these orbitals exist and why they have the shapes they do.

The Influence of Electron Spin

Beyond the energy levels and orbital shapes, quantum mechanics also accounts for the intrinsic angular momentum of the electron, known as spin.

Electron spin is a purely quantum mechanical phenomenon with no classical analog. It’s as if the electron is spinning on its axis, even though it’s not a physical rotation.

Spin is quantized, meaning an electron can only have one of two spin states, often referred to as "spin up" and "spin down."

The inclusion of electron spin in quantum mechanical calculations leads to a further refinement of the energy levels, known as fine structure. This fine structure splits the energy levels into slightly different sublevels, which can be observed through high-resolution spectroscopy.

In essence, quantum mechanics is the bedrock upon which our understanding of atomic structure rests. It provides the theoretical justification for the existence of energy levels, atomic orbitals, and electron spin, transforming our view of the atom from a simple, indivisible particle to a complex and dynamic quantum system.

Spectroscopy offers compelling evidence for the quantized nature of atomic energy levels. But to truly grasp why these levels exist and why electrons behave as they do within atoms, we need to delve into the realm of quantum mechanics. Now, having explored the theoretical underpinnings and the experimental techniques that reveal the structure of atoms, it’s time to turn our attention to the tangible benefits of this knowledge. Where does the understanding of energy sublevels lead us in the real world?

Applications: The Real-World Impact of Energy Sublevel Knowledge

The intricate dance of electrons within atoms, governed by the principles of quantum mechanics and expressed through energy sublevels, isn’t just an abstract theoretical concept. It has profound and practical implications across numerous scientific and technological domains. The ability to understand and manipulate these sublevels is the key to unlocking a wide range of applications that shape our modern world.

Chemical Bonding and Molecular Properties

The very foundation of chemistry – the formation of chemical bonds – is rooted in the interactions of electrons occupying specific energy sublevels. The way atoms share or transfer electrons to achieve stable electron configurations directly dictates the type of bond formed (ionic, covalent, metallic) and the resulting properties of the molecule.

Understanding the energy sublevels involved allows chemists to predict the strength and stability of chemical bonds, as well as the geometry and polarity of molecules. This predictive power is essential for designing new molecules with desired properties.

Consider the design of new drugs.

Pharmaceutical chemists use their knowledge of energy sublevels and molecular orbital theory to predict how a drug molecule will interact with specific biological targets, such as enzymes or receptors.

This rational drug design approach significantly speeds up the drug discovery process and increases the likelihood of success.

Materials Science: Designing the Future, Atom by Atom

Materials science is another field heavily reliant on understanding energy sublevels. The properties of materials, such as their conductivity, strength, and optical behavior, are all determined by the arrangement of electrons in their constituent atoms and how these atoms interact with each other.

For example, the conductivity of a metal depends on the availability of electrons in partially filled energy bands.

These bands are formed by the overlap of atomic orbitals from many atoms. By manipulating the composition and structure of materials at the atomic level, scientists can tailor their electronic band structures and, consequently, their properties.

This principle is used in the development of:

• Semiconductors for electronics.
• Superconductors for lossless energy transmission.
• Advanced alloys for aerospace applications.

The ability to design materials with specific properties is revolutionizing industries ranging from energy to transportation.

Predicting and Controlling Chemical Reactions

Understanding energy sublevels is crucial for predicting and controlling chemical reactions. Chemical reactions involve the rearrangement of electrons and atoms, and the energy changes associated with these rearrangements are dictated by the energy levels of the participating electrons.

By analyzing the electron configurations of reactants and products, chemists can predict the feasibility and rate of a reaction.

This knowledge is used to:

• Optimize reaction conditions.
• Design catalysts that accelerate reactions.
• Develop new synthetic routes for producing valuable chemicals.

For example, catalytic converters in automobiles rely on carefully designed catalysts to convert harmful pollutants into less harmful substances. These catalysts are designed based on a detailed understanding of the electronic structure of the catalyst materials and the reaction intermediates.

Atomic Physics and Fundamental Research

The study of energy sublevels is also at the heart of fundamental research in atomic physics. Precise measurements of energy level transitions provide valuable insights into the fundamental constants of nature and test the predictions of quantum electrodynamics (QED), the most accurate theory in physics.

Furthermore, the development of advanced technologies such as:

• Atomic clocks.
• Quantum computers.

Relies on the ability to precisely control and manipulate the energy levels of atoms. Atomic clocks, for example, use the extremely stable and well-defined energy transitions in atoms to achieve unparalleled accuracy in timekeeping.

Quantum computers leverage the superposition and entanglement of quantum states, which are directly related to the energy levels of qubits (quantum bits), to perform computations that are impossible for classical computers.

Understanding and controlling energy sublevels is therefore pushing the boundaries of scientific knowledge and enabling the development of revolutionary technologies.

Beyond the Horizon: Future Applications

The applications of energy sublevel knowledge are continuously expanding. As our ability to manipulate matter at the atomic level increases, we can expect even more groundbreaking discoveries and innovations in the future. From developing new energy sources to creating advanced medical diagnostics, the power of understanding energy sublevels will continue to shape the world around us.

So, that’s the lowdown on energy sub level! Hopefully, you now have a better grasp of how these tiny energy divisions shape the world around us. Go forth and explore the fascinating world of atoms!