Circle Diameter Formula: The Ultimate Guide You Need

Understanding circles is fundamental in geometry, and calculating their diameter is a crucial skill. The circle dia formula, derived from the core principle of Euclidean geometry, provides a straightforward method to determine this key measurement. Specifically, this formula allows you to find the diameter by knowing the radius. Practical applications of this formula extend beyond theoretical math, and are used in engineering and design for instance. With this information, the world, or at least the circles within it, gets a lot smaller.

Understanding the Optimal Article Layout for the "Circle Diameter Formula"

This guide outlines the ideal layout for an article titled "Circle Diameter Formula: The Ultimate Guide You Need," focusing on clarity, comprehensiveness, and effective keyword integration. The goal is to create an informative and user-friendly resource that thoroughly explains the "circle dia formula" to readers of varying mathematical backgrounds.

1. Introduction: Setting the Stage

The introduction should immediately capture the reader’s attention and clearly state the article’s purpose.

• Start with a relatable scenario or question: "Have you ever needed to find the size of a round table to fit in your dining room? Or perhaps you’re designing a circular garden bed? The circle dia formula is key to solving these, and many other real-world problems."
• Clearly define "diameter": "The diameter of a circle is the straight line that passes through the center of the circle, connecting two points on its edge."
• Briefly introduce the formula and its importance: "This guide will provide a comprehensive understanding of the circle dia formula, its variations, and its practical applications."
• Outline what the reader will learn: "By the end of this article, you’ll be able to confidently calculate the diameter of any circle, regardless of the information you’re given."

2. The Fundamental Circle Diameter Formula

This section introduces the core formula.

2.1. Diameter and Radius Relationship

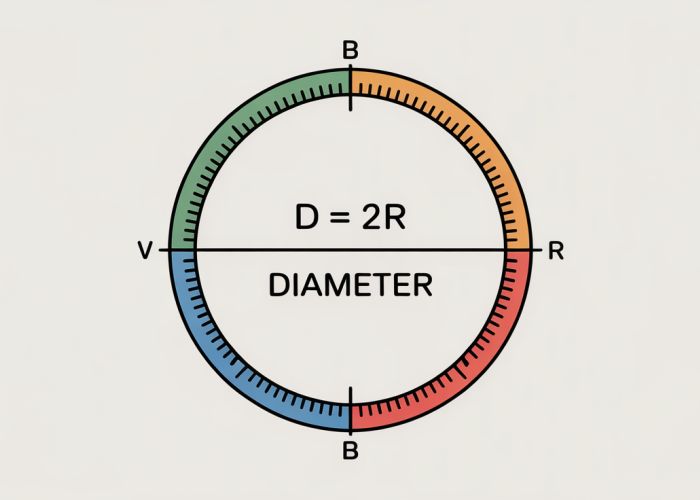
• Explain the relationship between diameter (d) and radius (r): "The diameter is twice the length of the radius. Conversely, the radius is half the length of the diameter."
• Introduce the circle dia formula related to the radius: d = 2r.
• Provide a simple example: "If a circle has a radius of 5 cm, then its diameter is 2 * 5 cm = 10 cm."

2.2. Diameter and Circumference Relationship

• Introduce the concept of circumference (C): "The circumference is the distance around the circle."
• Introduce the mathematical constant Pi (π): "Pi (π) is a constant approximately equal to 3.14159." Explain that it represents the ratio of a circle’s circumference to its diameter.
• Present the circle dia formula related to circumference: d = C / π.
• Work through an example: "If a circle has a circumference of 31.4 cm, then its diameter is 31.4 cm / π ≈ 10 cm."
• Include a cautionary note regarding rounding Pi: "Be mindful of rounding errors when using approximate values of π. For greater accuracy, use a calculator with a π button or more decimal places."

3. Deriving the Circle Diameter Formula

This section aims to build deeper understanding by showing how the formula is derived.

3.1. Starting with the Circumference Formula

• Begin with the formula for circumference: C = πd.
• Explain the algebraic manipulation: "To isolate the diameter (d), we divide both sides of the equation by π."
• Show the resulting formula: d = C / π.

3.2. From the Radius Definition

• Reiterate the definition: "The diameter is defined as twice the radius: d = 2r."
• Emphasize the directness of this formula: "This formula requires no complex derivations; it’s a fundamental definition."

4. Practical Applications of the Circle Dia Formula

This section provides real-world examples to illustrate the formula’s usefulness.

4.1. Engineering and Design

• Bullet points highlighting applications:
  • Designing circular gears.
  • Calculating the size of pipes.
  • Determining the dimensions of circular components in machines.

4.2. Construction

• Bullet points showcasing relevance:
  • Calculating the amount of material needed for circular structures like domes.
  • Laying out circular patios or driveways.
  • Ensuring proper fit of circular windows or skylights.

4.3. Everyday Life

• Illustrative examples using tables:

  Scenario	Given Information	Applying the Circle Dia Formula	Solution
  Finding the size of a pizza pan.	Pizza circumference: 62.8"	d = C / π = 62.8 / π	Diameter ≈ 20 inches
  Measuring a coin.	Coin radius: 1 cm	d = 2r = 2 * 1	Diameter = 2 cm

5. Solving Problems Using the Circle Dia Formula: Step-by-Step

This section provides worked examples with detailed explanations.

5.1. Example 1: Finding Diameter from Circumference

• Problem statement: "A circular swimming pool has a circumference of 78.5 meters. What is its diameter?"
• Step-by-step solution:
  1. "Identify the given information: C = 78.5 meters."
  2. "Recall the formula: d = C / π."
  3. "Substitute the value: d = 78.5 / π."
  4. "Calculate: d ≈ 25 meters."
  5. "Answer: The diameter of the swimming pool is approximately 25 meters."

5.2. Example 2: Finding Diameter from Radius

• Problem statement: "The radius of a Ferris wheel is 30 meters. What is its diameter?"
• Step-by-step solution:
  1. "Identify the given information: r = 30 meters."
  2. "Recall the formula: d = 2r."
  3. "Substitute the value: d = 2 * 30."
  4. "Calculate: d = 60 meters."
  5. "Answer: The diameter of the Ferris wheel is 60 meters."

6. Common Mistakes and How to Avoid Them

This section focuses on preventing errors in calculations.

• Mistakes listed in bullet points, with explanations of how to avoid them:
  • Using the radius instead of the diameter (or vice-versa) incorrectly: "Double-check which value is provided in the problem."
  • Forgetting to divide by π when using the circumference: "Always remember the formula d = C / π."
  • Using an inaccurate value of π: "Use a calculator with a π button for best accuracy."
  • Incorrect unit conversions: "Ensure all measurements are in the same units before calculating."

7. Advanced Applications (Optional)

This section is for readers who want a deeper dive. Can be omitted if the target audience is beginners.

7.1. Diameter in Circle Theorems

• Briefly mention how the diameter features in theorems like Thales’s Theorem.

7.2. Diameter and Area Calculation

• Show how the diameter can be used to derive the area: Area = π * (d/2)^2.

Alright, that wraps up our deep dive into the circle dia formula! Hope it cleared things up and makes tackling those circle problems a little easier. Go forth and measure with confidence!